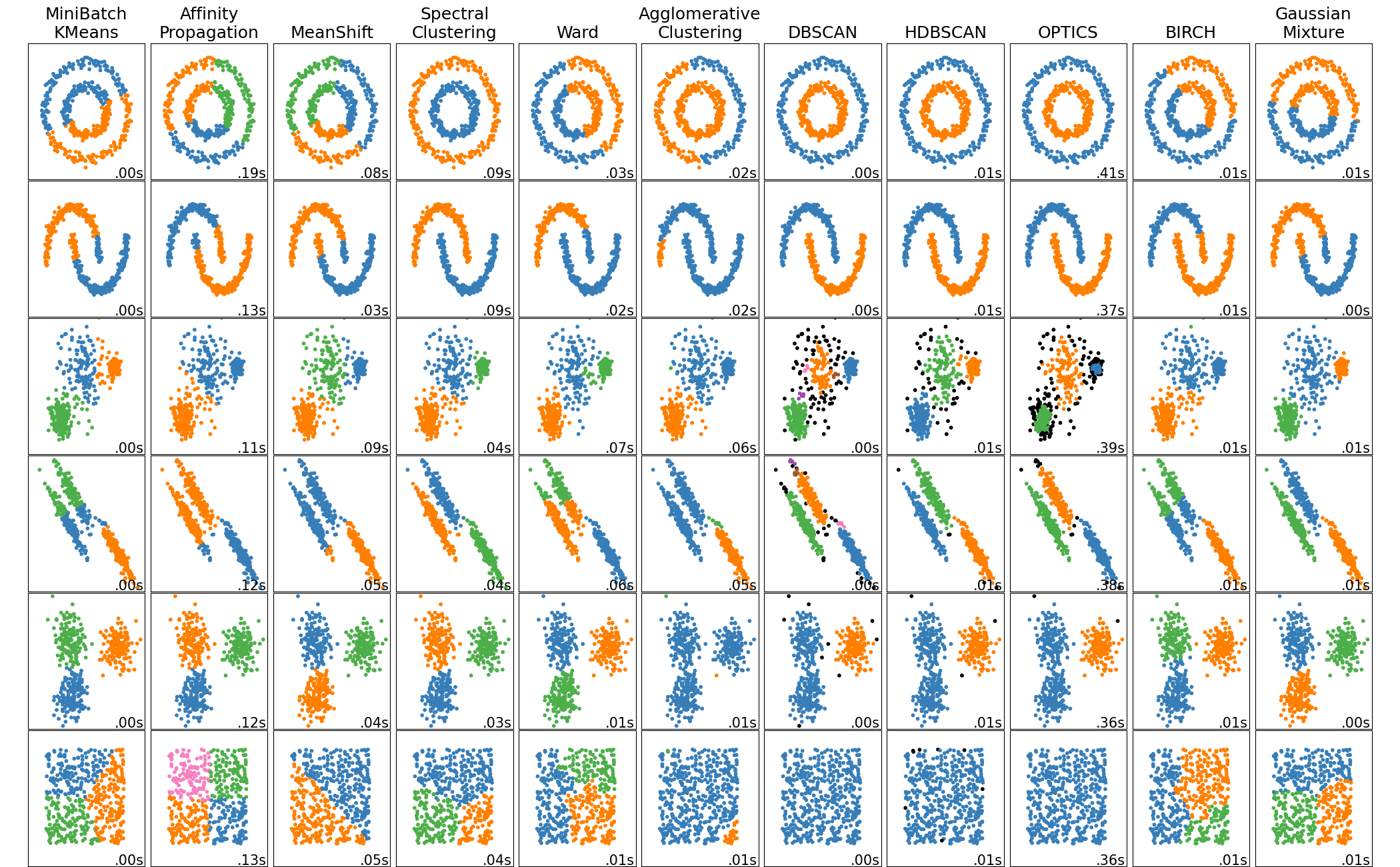
Clusterting

정의 : 두개의 오프젝트 사이의 similarity를 측정하기 위해서 두 오브젝트 사이의 거리(distance, dissimilarity)를 측정

  • 두 오프젝트 사이의 거리(distance) : 한 개의 object에서, 다른 한 개의 object으로 변화되기 위하여 필요한 노력(effort)를 측정한다.

접근 방법

  1. Compactness
    • 서로 가까이 있는 대상은 같은 그룹으로 묶이고, 그 그룹의 핵을 중심으로 같은 그룹에 포함된 대상들이 밀집되어 분포하도록 하는 방식입니다.
    • 주로 두 대상간의 거리 ( 유클리드 거리 등 ) 가 대상간의 유사도를 측정하는 척도로 사용됩니다.
    • K-Means 알고리즘이 이 분류의 알고리즘에 속합니다.
  2. Connectivity
    • 서로 연결되어 있거나 바로 옆에 있는 대상이 같은 그룹으로 묶입니다.
    • 두 대상의 거리가 매우 가깝더라도 대상이 연결되어 있지 않다면 같은 그룹으로 묶이지 않습니다.
    • Spectral Clustering 알고리즘이 이 방법을 사용한 클러스터링 알고리즘에 해당합니다.

1.0 유사도 계산

분류

  • 민코스키 거리 : 벡터 공간 안의 두점 사이의
  • 마하라노비스 거리 : 점들의 분호를 고려한 거리

A. 민코스키 거리

p=1 : 맨하탄(=L1) : (실질적으로) x축으로 이동 거리, y축으로 이동 거리, 보라색 p=2 : 유클리드(=L2) 거리 : (우리가 일반적으로 아는) 두 점사이의 직선 거리, 초록색

B. 마할라노비스 거리

두점 사이의 거리를 계산할때 데이터의 분포를 고려하는 거리

두 좌표값의 단위가 다른(키 & 몸무게)경우 각 축간의 공분산을 고려

  • 공분산 고려 = X값의 증감과 Y값의 증감의 관계를 거리에계산에 넣기

공분산 : 두 변수가 얼마나 연관성이 있는지 나타내는 값,

[Distance function 과 Similarity function의 예]

image image image

clustering valuation(군집 모델 평가하기): ARI, NMI

1.1 분류

  • 중심 기반 군집화 : 클러스터를 클러스터 중심점으로 정의하는 기법
  • 계측적 군집화 : 클러스터의 크기에 따라 클러스터의 계층을 정의하고 계층의 상하위를 이용하는 기법
  • 밀도 기반 군집화 : 클러스터를 데이터가 높은 밀도로 모여 있는 공간으로 보는 기법

EM 알고리즘( Expectation Maximization)은 어디에 속하나??

A. 중심 기반 군집화

가. K-중심 군집화 (k-centroid, k-medoid)

클러스터 중심점을 정한 후 가까운것 데이터들을 모아가며 클러스터를 확장

분류 : 중심값을 구하는 방법에 따라

  • k-mean(평균) 군집화
  • k-median(대푯값) 군집화
  • k-mode(최빈값) 군집화

B. 계측적 군집화

최상의 계층 클러스터 : 모든 데이터를 포함하는 하나의 클러스터 최하의 계층 클러스터 : 단 하나의 데이터만을 포함하는 데이터 수만큼의 클러스터

분류

  • 하향식 : 분할적 군집화
  • DIANA(Divisive Analysis)
  • 상향식 : 집괴적 군집화

특징

  • 클러스터 수를 지정할 필요가 없음

동작 과정 1. 하나의 데이터를 하나의 클러스터로 지정 2. 과정 1의 클러스터들에 대해 가장 유사도가 높은 클러스터 둘을 하나로 합침 3. 과정 2에서 생성된된 클러스터들에 대해 다시 같은 과정을 반복

클러스터를 합치는 방법 : 클러스터간의 유사도 측정

  • 단일 연결법 : 가장 짧은 거리를 클러스터 사이의 거리로 간주
  • 완전 연결법 : 가장 먼 거리를 클러스터 사이의 거리로 간주
  • 평균 연결법 : 데이터 들의 거리 평균을 클러스터 사이의 거리로 간주

C. 밀도 기반 군집화

데이터 밀도가 높아지는 방향으로 데이터를 군집화 하는 방식

가. 평균이동 군집화

동작 과정

  1. 임의의 초기 중심점 지정, 탐색 반경 지정
  2. 지정한 중심점에서 지정된 탐색 반경의 밀집도 계산
  3. 밀집도 높은 쪽으로 중심점 재 지정
  4. 반복

중심점을 이동한다는 측면에서 일부에서는 중심기반 군집화로 분류 하기도 함

나. DBSCAN

TBD

My best guess from your description is that you have 100 data streams, all providing x,y,z data from different sources? What do you mean by 'cluster them'? Do you mean group data with similar x,y,x values? Or do want similar x,y,z values at a 'similar time' - in this case it is simply 4D data, time is just another dimension. Also, do you want hyper-elliptical clusters, or arbitary shapes of connected similairty? Considerations: You first have to consider what you mean by 'cluster'? What do you define as a cluster? You then have to consider how many clusters you want? A fixed number, or an appropriate number based on the data spread or clusters of fixed sizes? You then have to consider the importance of outliers - do you want to force them into the nearest custer, discard them or are they actually the most important data points? Then consider when you want to cluster? Offline after data collection, on-line during data collection or at discreet time intervals? If on-line how do you want the clusters to behave? To grow, move and be created based on all data so far or to fully evolve and allow clusters that are no longer receiving data to 'fade and die out'. Depending on your answers to these questions different techniques are more appropriate, e.g.

Hierarchical - not really any use for anything except small, offline data sets as it takes waaaay too much memory
Subtractive - offline, finds an appropriate number of clusters, but slow
k-means - only useful if you have a fixed number of clusters and don't mind data being forced into clusters it doesn't belong in
DBScan - has a number of variants, offline will find arbitrary shaped clusters
ELM - online evolving hyper-elliptical clusters
My techniques:
DDC - very fast offline approach that will find an appropriate number of clusters
DDCAR - very fast offline and will find appropriate clusters with no user input whatsoever but is limited to hyper-spherical clusters
DDCAS - DDC adapted for arbitrary shaped clusters (unpublished as yet so you can't have any source code but I can run it for you)
CODAS - very fast, online and will find the required number of clusters and clusters of arbitrary shape (unpublished as yet so you can't have any source code but I can run it for you)

All of these are available for Matlab: hierarchical, subtractive and k-means are built in an implementation of DBScan is available online, I forget where DDC & DDCAR I have almost finished tidying up to a releasable version DDCAS & CODAS - I can run for you on test data There are also various implementations of other technqieus around including Matlab Central File Exchange

비교 방법

Comparing different clustering algorithms on toy datasets

results matching ""

    No results matching ""