차원 축소의 장점
- 데이터 노이즈를 없애줌
- 학습 알고리즘의 결과를 더 좋게 만들어 줌
- 데이터세트를 다루기 쉽게 만들어 줌
- 결과를 이해하기 쉽게 만들어줌
차원 축소의 3가지 방법
Feature Selection : 상관관계 분석등을 통한 유용한 피처 선택
Feature derivation : 기존 피처를 사용하여서 새로운 피처 생산
군집화 : 비슷한 데이터 점들을 모아 보는것
1. 선형 판별 분석 (LDA: Linear Discriminant Analysis)
지도학습에 목적을 둔 차원 축소 방법 1936년 R.A 피셔
정의 : 공분산(데이터 안에 분포 정도 표현)을 이용해서 데이터의 흩어진 정보를 이해, 클래스간의 분별 정보를 최대한 유지 시키면서 축소
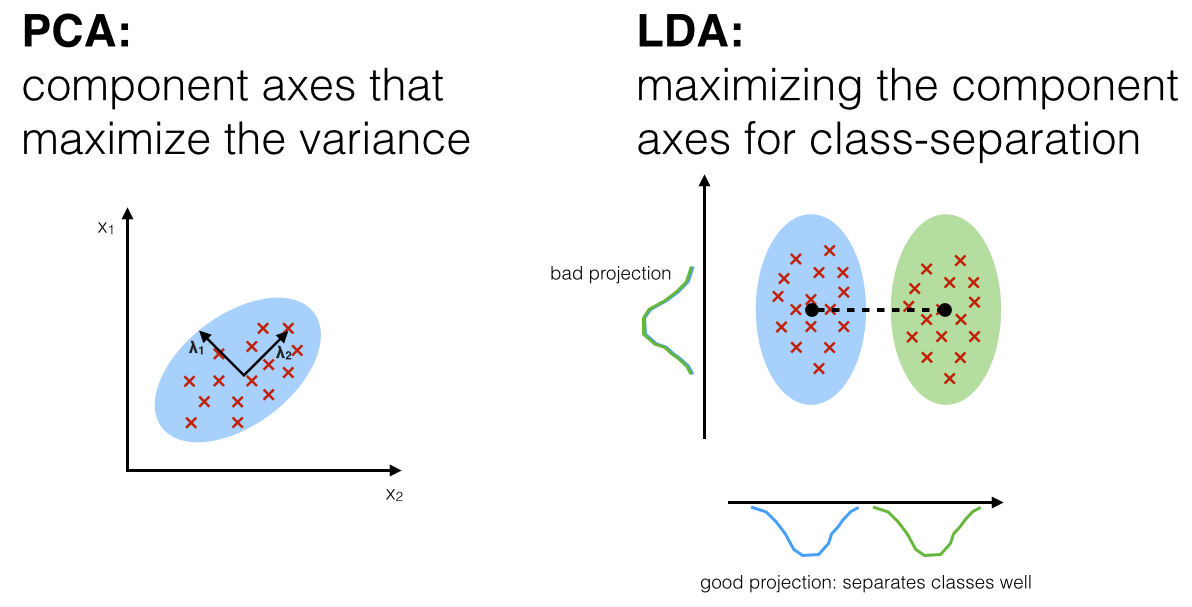
PCA는 데이터의 최적 표현의 견지에서 데이터를 축소 하는 방법인데 반하여, LDA는 데이터의 최적 분류의 견지에서 데이터를 축소 하는 방법 임
2. 주성분 분석 (PCA: Principle Component Analysis)
Label이 없는 데이터에 사용 가능한 방법 (Label있는 데이터도 가능)
- PCA는 데이터에 많은 변수가 있을때 변수의 수를 줄이는 차원 감소 기법중 하나 얼굴 인식 분야에서 가장 보편 적으로 사용, 다중공선성 문제 해결에 활용 가능
- PCA는 변수들을 주성분이라 부르는 선형적인 상관관계가 없는 다른 변수들로 재표현
- 주성분들은 원 데이터의 분산을 최대한 보존하는 방법으로 구함
- PCA는 선형적으로 상관관계가 없는 독립된 변수들을 찾는 기법
- Princomp()함수 사용 :
- 범주 레벨의 수가 많다면 One Hot Encoding(model.matrix())사용
동작 순서
- 전체 데이터의 평균을 구한후 데이터에서 평균을 빼서 점들을 중앙으로 옮긴다.
- 남아 있는 데이터의 변화량을 살펴 보고 (1)과 수직인 또 다른 축을 찾아서 변화량을 가장 많이 포함하는 직선 그린다.
- 공분산 행렬을 만든다. (공분산 행렬은 모든 요소의 공통된 부분을 뺀 개별적 특징이 포함된 데이터라고 표현할 수 있다.)
- 공분산 행렬을 이용해 Eigen value와 Eigen vector를 구한다
- 전체 데이터를 Eigen vector에 Projection한다 (= Projection matrix(eigen vecto들의 모음)을 모든 데이터에 곱한다)