cbu01_탐색과 최적화

출처 : 충북대학교 이건명 교수, 자료1, 자료2

상태공간과 탐색

1. 탐색 정의

문제의 해가 될수 있는 것들의 집합을 공간으로 간주하고, 문제에 대한 최적의 해를 찾기 위해 공간을 체계적으로 찾아 보는것
- 해(solution)정의 : 일련의 동작으로 구성되거나 하나의 상태로 구성
- 상태(state)정의 : 특정 시점에 문제의 세계가 처해 있는 모습
- 세계(world)정의 : 문제에 포함된 대상들과 이들의 상황을 포괄적으로 지칭

2. 상태공간(State Space) 정의

문제 해결과정에서 초기 상태로부터 도달할 수 있는 모든 상태들의 집합
문제의 해가 될 가능성이 있는 모든 상태들의 집합
- 초기 상태: 문제가 주어진 시점의 시작 상태
- 목표 상태: 문제에서 원하는 최종 상태

탐색문제의 예

선교사-식인종 강건너기 문제
8퍼즐 문제
tic-tac-toe

3. 상태공간 그래프(State space graph)

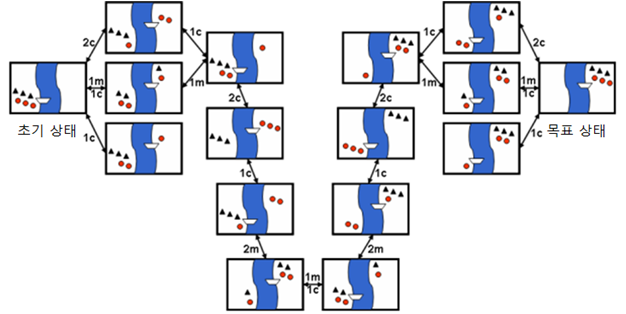
상태공간에서 각 행동에 따른 상태의 변화를 나타낸 그래프
- 노드 : 상태
- 링크 : 행동
- 해 : 초기상태에서 목표 상태로의 경로
문제점 : 일반적인 문제에서는 상태 공간이 매우 큼
- 미리 상태 공간 그래프를 만들기 어려움

인공지능에서는 탐색과정에서 그래프 생성함

정해진 순서에 따라 상태 공간 그래프를 점차 생성해 가면서 해를 탐색하는 방법

1 : 깊이 우선 탐색(depth-first search, DFS)

초기 노드에서 시작하여 깊이 방향으로 탐색
목표 노드에 도달하면 종료
더 이상 진행할 수 없으면, 백트랙킹(backtracking, 되짚어가기)
방문한 노드는 재방문하지 않음
메모리 적게 소모
최단 거리를 보장 하지 않음

2 : 너비 우선 탐색(breadth-first search, BFS)

초기 노드에서 시작하여 모든 자식 노드를 확장하여 생성
목표 노드가 없으면 단말노드에서 다시 자식 노드 확장
전체 트리를 메모리에서 관리, 메모리 부담 큼
최단 거리를 보장해 줌

3. 반복적 깊이심화 탐색(iterative-deepening search)

깊이/너비 우선 탐색의 장점만 활용(메모리, 최단거리)
깊이 한계가 있는 깊이 우선 탐색을 반복적으로 적용
단점: 동일 노드들이 만들어짐, 크기 늘지는 않음

4. 양방향 탐색(bidirectional search)

초기 노드와 목적 노드에서 동시에 너비 우선 탐색을 진행
중간에 만나도록 하여 초기 노드에서 목표 노드로의 최단 경로를 찾는

방법

정보 이용 탐색(informed search)

휴리스틱 탐색(heuristic search)
언덕 오르기 방법, 최상 우선 탐색, 빔 탐색, A* 알고리즘 등

1. 휴리스틱(heuristic)

그리스어 Εὑρίσκω (Eurisko, 찾다, 발견하다, 유레카)
시간이나 정보가 불충분하여 합리적인 판단을 할 수 없거나,굳이 체계적이고 합리적인 판단을 할 필요가 없는 상황에서 신속하게 어림짐작하는 것
최적해를 보장 할수 없음
예 : 최단 경로 문제에서 목적지까지 남은 거리
- 현재 위치에서 목적지(목표 상태)까지 지도상의 직선 거리, 직선이라는 직관을 이용

2. 언덕 오르기 방법(hill climbing method)

지역 탐색(local search), 휴리스틱 탐색(heuristic search)
현재 노드에서 휴리스틱에 의한 평가값이 가장 좋은 이웃 노드(주변을 보면서) 하나를 확장해 가는 탐색 방법
- 활용 정보 : 이웃 노드의 높이
단점: 국소 최적해(local optimal solution)에 빠질 가능성

3. 최상 우선 탐색(best-first search)

확장 중인 노드들 중에서 목표 노드까지 남은 거리가 가장 짧은 노드를 확장하여 탐색
- 활용 정보 : 목표노드 상태와 다른 것
남은 거리를 정확히 알 수 없으므로 휴리스틱 사용
Best인거 하나만 활용

4. 빔 탐색(beam search)

휴리스틱에 의한 평가값이 우수한 일정 개수의 확장 가능한 노드만을 메모리에 관리하면서 최상 우선 탐색을 적용
'최상 우선 탐색'과 비슷하나 Best인거 하나가 아닌 Good 여러개를 같이 선택

5. A* 알고리즘(A-star 알고리즘)

추정한 전체 비용 F(n)을 최소로 하는 노드를 확장해 가는 방법
f(n): 노드 n을 경유하는 전체 비용
- 현재 노드 n까지 이미 투입한 비용 g(n)과 목표 노드까지의 남은 비용 h(n)의 합
- f(n) = g(n) + h(n)
문제점 : 남은 비용 h(n)의 정확한 예측 불가
해결책 : h(n)에 대응하는 휴리스틱 함수 H(n)사용
- F(n) = g(n) + H(n)

게임에서의 탐색

1. 게임 트리(game tree)

상대가 있는 게임에서 자신과 상대방의 가능한 게임 상태를 나타낸 트리
- ex: 보드게임 = 틱-택-톡(tic-tac-toc), 바둑, 장기, 체스 등
게임의 결과는 마지막에 결정
많은 수(lookahead)를 볼 수록 유리

1.2 mini-max 알고리즘(mini-max algorithm)

MAX 노드
- 자신에 해당하는 노드로 자기에게 유리한 최대값 선택
MIN 노드
- 상대방에 해당하는 노드로 최소값 선택
단말 노드부터 위로 올라가면서 최소(minimum)-최대(maximum) 연산을 반복하여 자신이 선택할 수 있는 방법 중 가장 좋은 것은 값을 결정

1.2 a-b 가지치기 (prunning)

검토해 볼 필요가 없는 부분을 탐색하지 않도록 하는 기법
깊이 우선 탐색으로 제한 깊이까지 탐색을 하면서, MAX 노드와 MIN 노

드의 값 결정
- a-자르기(cut-off) : MIN 노드의 현재값이 부모노드의 현재 값보다 같거나 작으면, 나머지 자식 노드 탐색 중지
- b-자르기 : MAX 노드의 현재값이 부모노드의 현재 값보다 같거나 크면, 나머지 자식 노드 탐색 중지

게임트리 방법은 휴리스틱요소 필요, 직접 시뮬레이션 하면서 하기 위해 몬테카를로 방법 개발

2. 몬테카를로 트리 탐색(Monte Carlo Tree Search, MCTS)

탐색 공간(search space)을 무작위 표본추출(random sampling)을 하면서, 탐색트리를 확장하여 가장 좋아 보이는 것을 선택하는 휴리스틱 탐색 방법
4개 단계를 반복하여 시간이 허용하는 동안 트리 확장 및 시뮬레이션
- 선택(selection)
- 확장(expansion)
- 시뮬레이션(simulation) : 몬테카를로 시뮬레이션
- 역전파(back propagation)

알파고가 활용한 방법 중 하나

3.1 선택(selection) : 트리 정책(tree policy) 적용

루트노드에서 시작
정책에 따라 자식 노드를 선택하여 단말노드까지 내려 감
- 승률과 노드 방문횟수 고려하여 선택
- UCB(Upper Confidence Bound) 정책 : UCB가 큰 것 선택

3.2 확장(expansion)

단말노드에서 트리 정책에 따라 노드 추가
예. 일정 횟수이상 시도된 수(move)가 있으면 해당 수에 대한 노드 추가

3.3 시뮬레이션(simulation)

기본 정책(default policy)에 의한 몬테카를로 시뮬레이션 적용
무작위 선택(random moves) 또는 약간 똑똑한 방법으로 게임 끝날 때까지 진행

3.4 역전파(backpropagation)

단말 노드에서 루트 노드까지 올라가면서 승점 반영

특징

판의 형세판단을 위해 휴리스틱을 사용하는 대신, 가능한 많은 수의 몬테카를로 시뮬레이션 수행
일정 조건을 만족하는 부분은 트리로 구성하고, 나머지 부분은 몬테카를로 시뮬레이션
- 가능성이 높은 수(move)들에 대해서 노드를 생성하여 트리의 탐색 폭을 줄이고, 트리 깊이를 늘리지 않기 위해 몬테카를로 시뮬레이션을 적용
- 탐색 공간 축소

몬테카를로 시뮬레이션 (Monte Carlo Simulation)
- 특정 확률 분포로 부터 무작위 표본(random sample)을 생성하고, - 이 표본에 따라 행동을 하는 과정을 반복하여 결과를 확인하고, - 이러한 결과확인 과정을 반복하여 최종 결정을 하는 것
모든 경우를 수행 하면서 특정 수에서 이길 확률 정리하고 이를 이용하여 정리

제약조건 만족 문제(constraint satisfaction problem)

주어진 제약조건을 만족하는 조합 해(combinatorial solution)를 찾는 문제
탐색 기반의 해결방법
1. 백트랙킹 탐색
2. 제약조건 전파

1. 백트랙킹 탐색(backtracking search)

깊이 우선 탐색을 하는 것처럼 변수에 허용되는 값을 하나씩 대입
모든 가능한 값을 대입해서 만족하는 것이 없으면 이전 단계로 돌아가서 이전 단계의 변수에 다른 값을 대입

2. 제약조건 전파(constraint propagation)

인접 변수 간의 제약 조건에 따라 각 변수에 허용될 수 없는 값들을 제거하는 방식

목적 함수

최적화(optimization): 여러 가지 허용되는 값들 중에서 주어진 기준(=목적함수)을 가장 잘 만족하는 것을 선택하는 것
목적함수(objective function): 기준을 나타내는 함수, 최소 또는 최대가 되도록 만들려는 함수

조합 최적화 (combinatorial optimization)

순회 판매자 문제(TSP)와 같이 주어진 항목들의 조합으로 해가 표현되는 최적화 문제
- 목적함수 : 경로의 길이

NP-Hard Problem: 다 해보지 않고는 최적해를 알수 없음

일반적으로 최적해가 아닌 준-최적해를 주로 찾음 : 유전알고리즘,

1. 유전 알고리즘(genetic algorithm, GA)

생물의 진화를 모방한 집단 기반의 확률적 탐색 기법(John Holland, 1975)
대표적인 진화 연산(evolutionary computation)의 하나
- 유전 알고리즘, 유전자 프로그래밍(genetic programming), 전화 전략(evolutionary strategy)
최적해 보장은

[생물의 진화]
염색체(chromosome)의 유전자(gene)들이 개체 정보 코딩

적자생존(fittest survival)/자연선택(natural selection)
– 환경에 적합도가 높은 개체의 높은 생존 및 후손 번성 가능성
– 우수 개체들의 높은 자손 증식 기회
– 열등 개체들도 작지만 증식 기회

집단(population)의 진화
– 세대(generation) 집단의 변화

형질 유전과 변이
– 부모 유전자들의 교차(crossover) 상속
– 돌연변이(mutation)에 의한 변이

[참고] 생물 진화와 문제 해결의 관계

개체 = 후보 해(candidate solution)
환경 = 문제(problem)
적합도 = 해의 품질(quality)

[초기 모집단 생성]

모집단(population) : 동시에 존재하는 염색체들의 집합

(적합도 함수, fitness function)

후보해가 문제의 해(solution)로서 적합한 정도를 평가하는 함수

[부모 개체 선택(selection)]

높은 적합도의 개체가 새로운 개체를 생성할 확률이 높도록 함
적합도에 비례하는 선택확률
- 예. 개체 1의 적합도: 10, 개체 2의 적합도: 5, 개체 3의 적합도: 15

(유전 연산자, genetic operator)

새로운 개체 생성

(유전 알고리즘)

세대(generation) 교체 : 엘리트주의(elitism)
- 우수한 개체를 다음 세대에 유지

2. 메타 휴리스틱

특징

최적해(optimal solution)을 보장하지는 않지만 준최적해(suboptimal solution)을 빠르게 찾는 알고리즘

종류

유전 알고리즘
모방 알고리즘(memetic algorithm)
입자 군집 최적화(particle swarm optimization, PSO)
개미 집단(ant colony) 알고리즘
타부 탐색(Tabu search) : 이미 했던건 다시 안함
담금질 기법(simulated annealing)
하모니 탐색(Harmonic search)

함수 최적화

1. 함수 최적화 문제

정의

어떤 목적 함수(objective function)가 있을 때, 이 함수를 최대로 하거나 최소로 하는 변수 값를 찾는 최적화 문제

아래로 볼록한 함수(=Convex func)의 최적값은, 미분 = 0 하여 문제 풀이

2. 제약조건 최적화(constrained optimization)

참고 : 머신러닝에서 딥러닝까지, Deepcumen, 부록 A.2

정의

제약조건(constraints)을 만족시키면서 목적함수를 최적화시키는 변수값들을 찾는 문제

활용예

기계학습 방법인 SVM의 학습에서 사용


빨간선이 가능해	아래로 볼록한 함수(=Convex func)의 최적값은, `미분 = 0` 하여 문제 풀이

최적화 순서

Lagrange함수(제약조건 + 목적 함수 결함)정의로 시작

기존 제약 조건 + 목적함수에 임의의 라그랑주 승수 결합
라그랑주 승수 $\alpha$ 는 항상 0보다 커야 함

목적 재정의 : $min_{x_1x_2} \in FS f(X_1, X_2)$ 는 $L(x_1,x_2,\lambda, \alpha)$ 에 대해서 $\lambda, \alpha$ 를 가지고 최대화한 값을 $x_1, x_2$ 에 대해 최소한 값과 같은 것을 의미 한다.
min, max의 위치 변경하여 식 생성
- $min_{x_1,x_2} max_{\lambda, \alpha} L(x_1,x_2,\lambda, \alpha)$ = 큰것 중에 작은거 선택
- $max_{\lambda, \alpha} min_{x_1,x_2} L(x_1,x_2,\lambda, \alpha)$ = 작은것 중에 큰거 선택
- 큰것중에 작은거 선택한것이 크기 때문에 다음 식 생성 가능 : $min_{x_1,x_2} max_{\lambda, \alpha} \geq max_{\lambda, \alpha} min_{x_1,x_2}$
쌍대(Dual Function) 함수 찾기 : $min_{x_1,x_2} L(x_1,x_2,\lambda, \alpha) = L_d(\lambda, \alpha)$
식 재정의 : $min_{x_1,x_2} max_{\lambda, \alpha}L(x_1,x_2,\lambda, \alpha) \geq max_{\lambda, \alpha}L_d(\lambda, \alpha)$

결국 $min_{x_1x_2} \in FS f(X_1, X_2)$ 는 Dual function을 $\lambda, \alpha$ 에 대하여 최대화 하는 값을 찾으면 됨, 이와 함께 상보적 여유성도 만족 시키도록 함

최적화 예시

3. 회귀(regression) 문제의 최적 함수

주어진 데이터를 가장 잘 근사(近似, approximation)하는 함수
최소 평균제곱법(least mean square method)
- 오차 함수(error function) 또는 에너지 함수(energy function)를 최소로 하는 함수를 찾는 방법

$E = \frac{1}{2N} \sum^n_{i=1}(y_1 - f(x_i))^2$ 에서 $\frac{1}{2N}$ 의 N은 수의 양이 많기 떄문에 (평균화??), 2는 이후에 미분시 사라지기 때문에 적용

일반적으로 E를 찾지 못하므로 최적화 문제방법으로 해결

4. 최대 경사법(gradient descent method, 경사 하강법)

함수의 최소값 위치를 찾는 문제에서 오차 함수의 그레디언트(gradient) 반대 방향으로 조금씩 움직여 가며 최적의 파라미터를 찾으려는 방법
- 그레디언트: 각 파라미터에 대해 편미분한 벡터 $\left(\frac{\partial E}{\partial a}, \frac{\partial E}{\partial b}\right)$
데이터의 입력과 출력을 이용하여 각 파라미터에 대한 그레디언트를 계산하여 파라미터를 반복적으로 조금씩 조정

활용 : 회귀모델, 신경망 등의 기본 학습 방법
단점 : 국소해(local minima)에 빠질 위험
해결책 : 개선된 형태의 방법 존재(conjugate gradient method 등)

cbu01_탐색과 최적화

cbu01_탐색과 최적화

상태공간과 탐색

1. 탐색 정의

2. 상태공간(State Space) 정의

3. 상태공간 그래프(State space graph)

맹목적 탐색(Blind search)

1 : 깊이 우선 탐색(depth-first search, DFS)

2 : 너비 우선 탐색(breadth-first search, BFS)

3. 반복적 깊이심화 탐색(iterative-deepening search)

4. 양방향 탐색(bidirectional search)

정보 이용 탐색(informed search)

1. 휴리스틱(heuristic)

2. 언덕 오르기 방법(hill climbing method)

3. 최상 우선 탐색(best-first search)

4. 빔 탐색(beam search)

5. A* 알고리즘(A-star 알고리즘)

게임에서의 탐색

1. 게임 트리(game tree)

1.2 mini-max 알고리즘(mini-max algorithm)

1.2 a-b 가지치기 (prunning)

2. 몬테카를로 트리 탐색(Monte Carlo Tree Search, MCTS)

3.1 선택(selection) : 트리 정책(tree policy) 적용

3.2 확장(expansion)

3.3 시뮬레이션(simulation)

3.4 역전파(backpropagation)

제약조건 만족 문제(constraint satisfaction problem)

1. 백트랙킹 탐색(backtracking search)

2. 제약조건 전파(constraint propagation)

목적 함수

조합 최적화 (combinatorial optimization)

1. 유전 알고리즘(genetic algorithm, GA)

2. 메타 휴리스틱

함수 최적화

1. 함수 최적화 문제

2. 제약조건 최적화(constrained optimization)

3. 회귀(regression) 문제의 최적 함수

4. 최대 경사법(gradient descent method, 경사 하강법)

results matching ""

No results matching ""