2.2 ICP 알고리즘

m_a개의 점을 포함하는 소스 점군(source point cloud) A를 mb개의 점을 포함하는 타갯 점군(target point cloud) B에 정합한다고 가정하자. 이 때 ICP 알고리즘은 그림 2처럼 여섯 단계로 이루어져\ 있으며, 각 단계는 다음과 같이 요약할 수 있다.

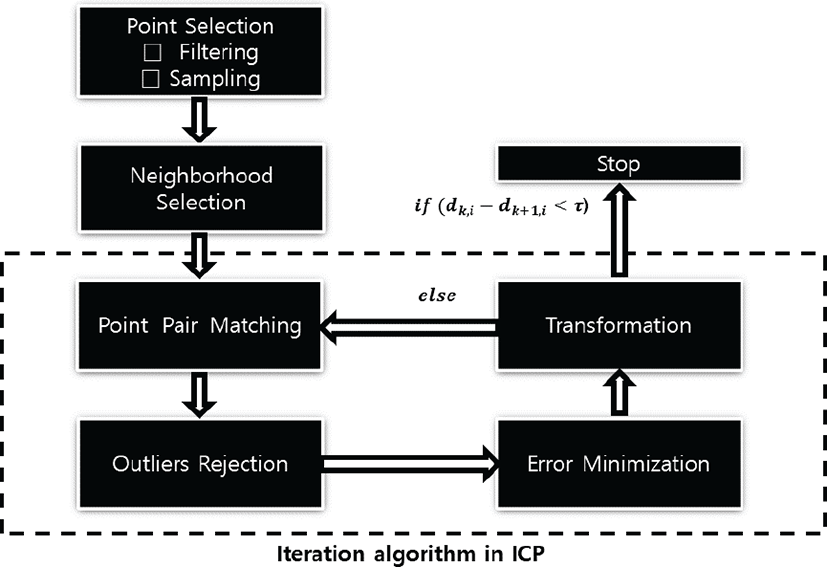
첫째, 점 선택(point selection) 단계에서는 알고리즘의 계산량을 줄이기 위하여 노이즈 필터링이나 샘플링을 거쳐 점의 갯수를 줄인다. 둘째, 이웃 선택(neighborhood selection) 단계에서는 각 점의 주변에 분포하는 점들 중 가까운 점 일부를 선택한다. 셋째, 점쌍 매칭(point pair matching) 단계에서는 앞서 선택한 주변 점들로 곡면(surface)[6]이나 평면(plane)[7] 같은 기하학 요소를 만들고, 이를 이용하여 소스 점군 A의 점 에 대응하는(corresponding) 타갯 점군 표의 점을 찾는다. 넷째, 오정합점 제거 (outlier rejection) 단계에서는 소스 점군 A와 타겟 점군 B에서 서로 겹치는 부분, 즉 오버랩 영역(inlier)만 남기고, 겹치지 않는 영역(outlier) 은 정합에 이용하지 않는다. 다섯째, 오차 최소화(error minimization) 단계 에서는 소스 점군 A의 오버랩 영역 A′과 타겟 점군 B의 오버랩 영역 B′ 방향으로 이동하는 동안 각 대응점의 거리 오차가 최소가 되도록 한다. 여섯째, 변환(Transformation) 단계에서 는 소스 오버랩 점군 A′가 타갯 오버랩 점군 B′의 위치로 이동하 는 데에 필요한병진 행렬(translation matrix)과 회전 행렬(rotation matrix)을 구하여 소스 오버랩 점군 A′에 적용한다. 여기서 거리 오차가 일정한 한계치(tolerance, τ) 이하이면 진행을 멈주고 한계치 이상이라면 점쌍 매칭 (point pair matching) 단계로 되돌아가서 알고리즘을 다시 수행한다.

이러한 ICP 알고리즘은 병진 3자유도와 회전 3자유도를 다루기 때문에 공간상의 모든 방향으로 적용할 수 있는 것은 물론, 점군 데이터의 국소 특징(local feature)이나 전처리(prepocessing)가 필요 없기 때문에 알고리즘이 비교적 간단하다는 장점을 가지고 있다[3]. 하지만 점쌍 매칭 단계에서 대응점 (corresponding point)을 찾는 과정이 알고리즘 1회 수행하는 데에 최대 O(mamb)의 복잡도를 보이는데다가, 오버랩 영역이 매우 적거나 없어 분할된 상태의 점군에 적용하면 정합이 잘못되는 경우가 허다하다[3]. 또, 성게처럼 형상이 복잡하거나[3] 사무용 건물 같이 반복되는 패턴의 경우에도 알고리즘을 적용하기 어렵다.

Besl은 회전 행렬을 구하는 데에 Horn의 최소 자승 사원수 연산(least square quaternion operation)[8]을 이용하여 변환 단계에 적용하였다[3]. 반면, Masuda는 오정합점 제거 단계에서 잔차의 표준 편차(standard deviation of residuals)를 도입하여 이 값의 2.5 배를 거리 임계값(distance threshold)로 설정하였다. 이 때 임계값 이하이면 정합점 (inlier)으로, 초과하면 오정합점 (outlier)으로 구 분하였다[9]. 여기서 Masuda는 샘플링이 일정하지 않은 무작위 샘플링(random sampling)을 사용한 반면, 본 논문에서는 균일 샘플링 (uniform sampling)을 사용하였다. 한편, Pulli는 점쌍 매칭 단계에서 정적 임계값(hard threshold) 내에서 대응점을 찾되, 각 점 군의 법선 벡터(compatible normal vector)의 사잇각이 45도 이하 이고, 대응점이 메시 경계(mesh boundary) 위에 있지 않는다면 오버랩 영역에 해당하는 동적 임계값(dynamic threshold)을 유지한 채 매칭 대칭(matching symmetric)을 만드는 경험적인(heuristic) 방법을 제안하였다[5]. 그러나 임계값들을 조절하며 많은 시행착오를 거쳐야 하기 때문에 원하는 정합을 얻기까지 오랜 시간이 걸린다는 단점을 안고 있다.