정리	동영상

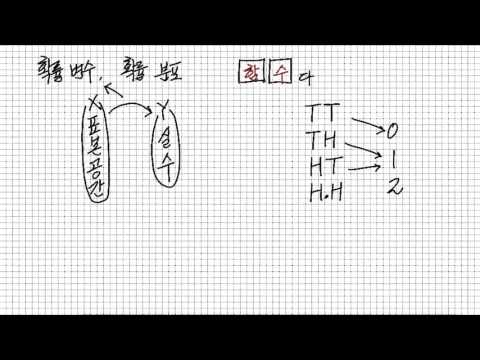
- 동전을 두번 던져 그림이 나오는 수를 X라 할때, X가 확률 변수 
- 확률 변수 X가 0을 가질 확률은 1/4....처럼 모든 확률 변수 X($$ X_0, X_1, X_2 $$)에 대한 확률(`1/4, 1/2, 1/4`)들의 분포를 ....확률 분포 
- 확률 변수 X를 확률로 맵핑 시키는 함수...확률 함수 

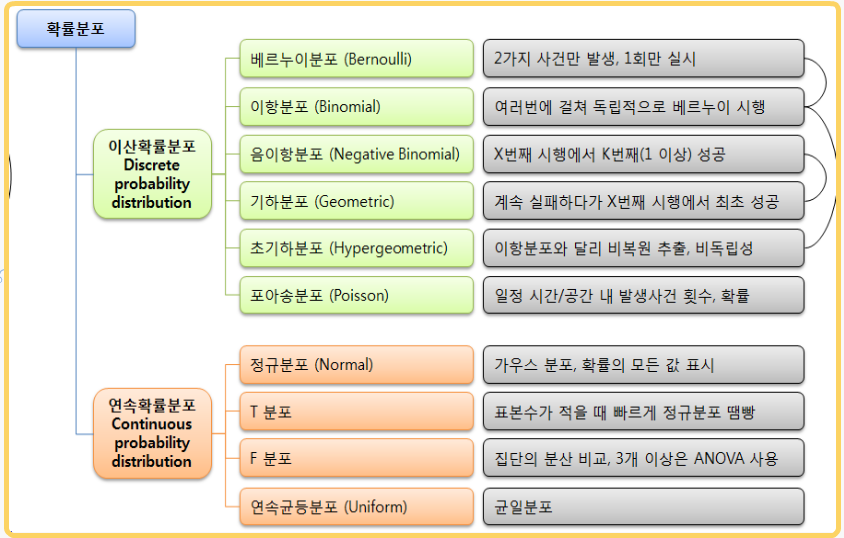
2. 확률 분포

확률 분포(probability distribution)

• 모든 확률 변수에 따라 나오는 값을 나열한것
• 확률 변수가 나올 확률 (eg, 1/4, 1/2)
• 확률 함수를 통해 도출

확률 분포표

• 확률 변수 x에 대한 확률을 도수 분포표로 만든것

확률 분포를 알아야 하는 이유 : 분포를 알아내면 전체 경향을 알수 있

통계적 가설검정에는 특정한 확률분포를 이용 (eg. 독립표본 T검정 = T분포, 분산분석 = F분포, 카이제곱검정 = 가이제곱 분포)

가설검정 프로세스

1. 관찰된 표본으로 부터 가설 검정을 위한 검정 동계량을 계산
2. 귀무가설이 옳다는 전제하에, 가정된 분포에서 관찰된 표본(검정통계량)이 발견된 수 있는 확률(P value=Provaility value)은 곡선의 아래 면적을 통해 알수 있다. = 유의 확률

표본 분포

• 표본 분포 : 모집단 전체가 아니라 표본을 뽑아서 만든 표본 통계량의 퍼진 형태
• 다른 확률 분포들이 확률을 구하는 것과 달리 표본 분포는 가설 검정시 사용
• T분포, 카이제곱 분포,F분포