 |
 |
|---|---|
| 정리 | 동영상 |
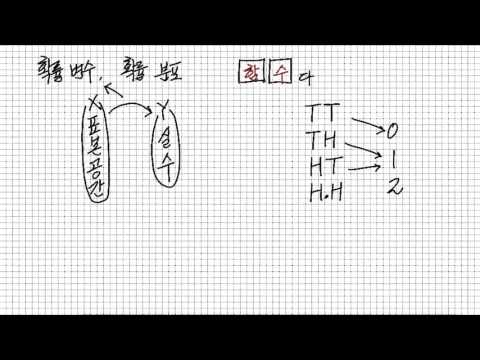
- 동전을 두번 던져 그림이 나오는 수를 X라 할때, X가 확률 변수
- 확률 변수 X가 0을 가질 확률은 1/4....처럼 모든 확률 변수 X($$ X_0, X_1, X_2 $$)에 대한 확률(`1/4, 1/2, 1/4`)들의 분포를 ....확률 분포
- 확률 변수 X를 확률로 맵핑 시키는 함수...확률 함수
1. 확률 변수
확률변수(Random variable): 확률에 따라 변하는 값 (변수 = 특정 조건에 따라 변하는 값)
- 표본 공간을 정의역(domain)으로 가지고 실수를 공역(range)으로 가지는 함수
- 즉 표본 공간의 모든 표본에 대해 어떤 실수 값을 붙인(할당한) 것이다.
- x를 사용할때 확률 P(X)를 구할수 있다면 X는 확률 변수
- 사용자 정의 실수(eg. 0,1,2, 앞면의 갯수, 변할 수 있음), 앞면이란 기준(??)
- 주사위를 던질때 나오는 수 : $$ X_1 \in {1,2,3,4,5,6} $$
- 주사위를 두번 던질때 나오는 수의 합 : $$ X_2 \in {2,3,4,...,11,12} $$
| 정의 | 임의로 정한 이름 | ex) 앞면이 나오면 0으로 정하자...0이 확률 변수 |
|---|---|---|
| 분류 | 확률 변수가 취하는 값의 종류에 따라(이산or연속) |

[확률 vs. 확률 변수]
- 확률은 표본으로 이루어진 집합 즉, 사건에 대해 할당된 숫자이지만 확률 변수는 표본 하나 하나에 대해 할당된 숫자이다.
- 확률은 0부터 1사이의 숫자만 할당할 수 있지만 확률 변수는 모든 실수 범위의 숫자를 할당할 수 있다.