B. 추론 통계 분석

  • 표본을 분석하여 모집간에 대해 추측하고 일반화 시키는 연구 분야
  • 새로운 가설이 틀지는지 맞는지 검증

1. 추정 (Estimation)

  • 테스트값을 모를경우에 표본의 평균과 표준오차를 통해 모수의 범위를 추측,
  • eg. 신뢰수준 95%의 확률로 ...

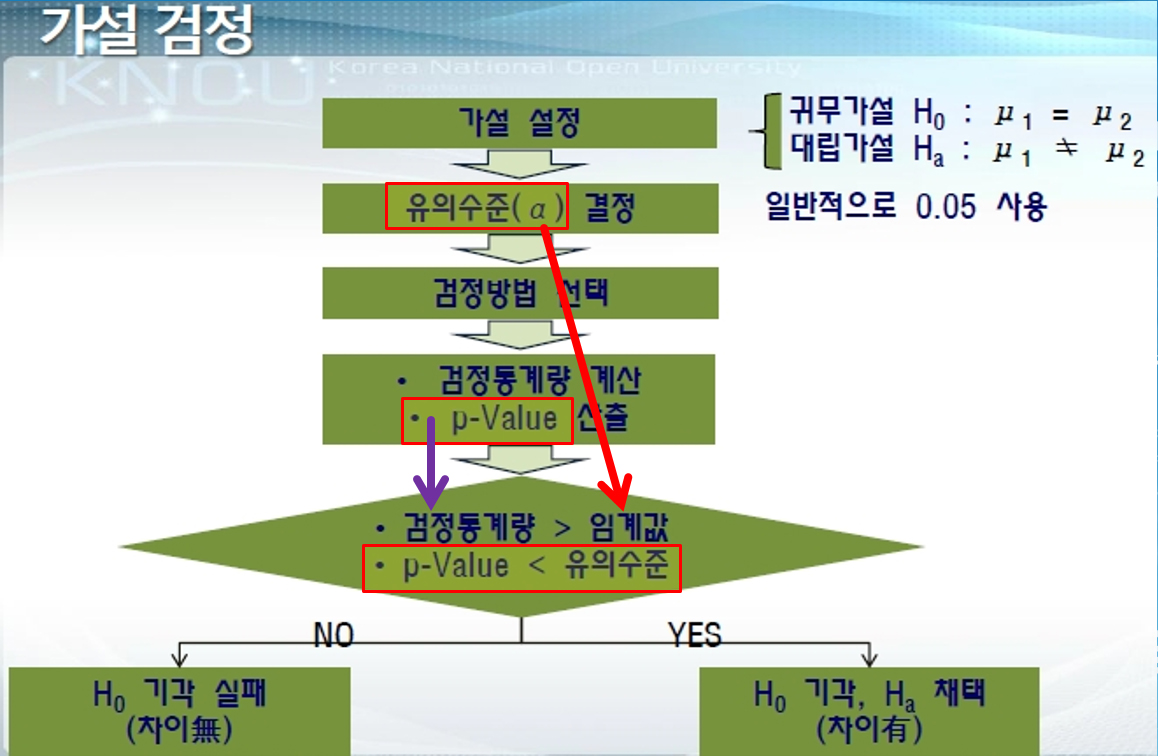
2. 가설검정 (Hypothesis Test)

  • 테스트값($$ \mu_0$$:모수일것으로 추측)이 있을 경우에 가설을 통해 테스트값의 진실 여부를 증명
  • 통계적 가설검정에서는 귀무가설을 받아들일 것인지, 아니면 기각할 것인지를 검증
  • 가설도 틀리수 있음 유의수준 5% 이내로
  • 가설 점정은 $$H_0$$가 진실 인지를 검증함
    • One sample t-test일 때, $$H_0 : \mu = \mu_0 $$
    • Independent Sample t-test 일 때, $$H_0 : \mu_1 = \mu_2 $$
    • Paired Sample t-test일 때,$$H_0 : \mu_d = 0 $$
    • Correlation Analysis일 때, $$H_0 : \rho = 0 $$

해석 : https://youtu.be/rnWkk93CKrQ?t=11m50s

[참고] 가설 검정의 오류
  • 1종 오류($$ \alpha$$) : 귀무가설이 참일때 이를 기각한다.(eg. 차이or효과가 없는데 차이or효과가 있다고 판단)
  • 2종 오류($$ \beta$$) : 귀무가설이 거짓일때 이를 받아들인다. (eg. 차이or효과가 있는데 차이or효과가 없다고 판단)

유의 수준 5%란? 2종 오류보다 1종 오류로 인한 사회적 파장이 큼 - 학계에서 1종 오류를 5% 미만으로 제한($$p < 0.05$$)

[참고] 유의수준/검정력/가설검정

유의수준($$\alpha$$)

  • $$\alpha$$를 이용한 검증 : $$H_0$$가 진실임을 증명
  • $$H_0$$가 진실인데 $$H_0$$을 기각할 수 있는 오류를 범할 확률의 최대 허용치
    • 0.01, 0.05,0.10 중 0.05(5%)

검정력(power)

  • $$\beta$$를 이용한 검증 : $$H_0$$가 것짓임을 증명
  • $$H_0$$가 거짓일 때 $$H_0$$를 기각할 수 있는 확률의($$1-\beta$$
    • 80~95%

가설 검정

  • $$\alpha$$는 현재사실을 근거로 검증하기 때문에 $$\beta$$를 통한 검증 보다는 $$\alpha$$를 이용한 가설검정을 실시
귀무가설($$H_0$$, Null Hypothesis, 영가설)
  • 아무일도 일어나지 않는다
  • 기존에 알려져 있는 사실, 현재의 가설
  • 평균 비교시 두 모집단의 평균이 같다.
  • 회귀 분석시 그래프의 기울기가 0이다.
  • 귀무가설은 반증이 가능해야한다는 점이 중요하다.
대립가설($$H_1$$, Alternative Hypothesis)
  • 어떤일이 일어난다.
  • 새로운 가설, 입증하려고 하는 주장

좋은 가설 = 기각이 가능한 가설=반증이 가능한 가설
by karl Popper

연구자가 증명하고자 하는 실험가설과 __반대__되는 입장, 증명되기 전까지는 효과도 없고 차이도 없다는 귀무가설을 세우고, 연구자가 실험을 통해 규명하고자 하는 가설인 대립가설을 세우고 
최종적으로 실험을 통해 귀무가설이 유의수준 5%미만이므로 발생확률이 적어 __기각_하고 대립가설을 __체택__하도록 하는게 목적임

3. p값(유의확률)

  • 가설 검증시 검정 통계량 사용
    • 검정 통계량 = 스튜던트 t, 피셔의 F, 피어슨의 카이제곱
  • p값은 검정 통계량의 크기에 대한 개념
    • eg. 귀무가설이 참이라 가정할 때 관심 사건의 검정 통계량을 계산하고 이 값과 같거나 큰 경우에 놓일 확률의 추정치가 바로 p값
    • 검정 통계량이 크다 = 귀무가설이 참일 것 같지 않음 = 귀무가설 기각하고 대립가설을 받아 들임
  • p-value는 귀무가설이 맞다는 전제 하에, 관측된 통계값 혹은 그 값보다 큰 값이 나올 확률이다.2

4. 모형 선택 : 아래의 가정들이 만족하여야 함(중요도 순)

  1. 무작위 표본 추출
  2. 등분산성
  3. 오차의 정규성
  4. 오차의 독립성
  5. 효과의 가산성

5. 최대 가능도(Maximum likelihood)

  • 모형이 데이터에 최적으로 적합될 때의 모수 값의 특징은
    • 편이가 없는, 분산을 최소화 하는 추정량 (Unbiased, variance minimizing estimators)

6. 시험 설계

  • 반복 실행 : 신뢰도 높이기 위해
  • 무작위화 : 편이(bias)를 줄이기 위해

올바른 분석을 시행하기 위해서는 아래 주제들도 고려 해야함

  • 간결성의 원칙
  • 검정력(power)
  • 통제집단
  • 인위적 반복(pseudoreplication)의 확인과 그에 대한 대처
  • 실험적 데이터와 관찰 데이터의 차이점(비직교성^non-orthogonality)

6.1 간결성의 원칙(오컴의 면도날)

  • 특정 현상에 대해 비슷한 설명들이 여러 개 있을 경우 가장 단순한 것을 선택 해야 한다.
    • 14세기 영국 유명론 철학자 윌리엄 오컴
    • 설명을 최소한으로 깍는다(shave)는 의미로 면도날이라고 불림
  • 통계 모형에서 간결성의 원칙은 다음의 의미를 포함한다.
    1. 모형은 되도록 가장 작은 수의 모수를 포함해야 한다.
    2. 비선형 모형보다는 선형 모형을 사용해야 한다.
    3. 되도록 작은 수의 가정을 고려할 수 있는 실험을 선택 해야 한다.
    4. 모형은 최소 합당한 수준까지 줄여야 한다.
    5. 복잡한 설명보다는 단순한 설명을 선택해야 한다.

6.2 반복 시행

  • 여러 번의 측정이 반복 시행으로 인정되려면 다음의 조건에 부합돼야 한다.
    1. 독립적이어야 한다.
    2. 시계열적 개념이 개입되어서는 안된다.
    3. 공간적인 독립성을 고려해야 한다.
    4. 적절한 공간 스케일을 사용해 측정이 이뤄져야 한다.
    5. 이상적으로는 각각의 처치들을 일정 기준의 블록으로 묶어 이를 각각의 시행으로 간주하고 이렇게 만들어진 많은 블록들에서 모든 처치들에 대한 측정이 이루어져야 한다.
    6. 동일한 개인이나 동일한 공간에서의 반복측정은 반복 시행이 아니다.

가설 검정 시 반복 시행 수는 어떻게 결정 하는가?

  • 보통 30번 정도 시행
  • 결정 방법론은???

6.3 검정력($$ 1-\beta$$)

  • 가설검정에서 귀무가설이 거짓일 때 이를 기각할 확률(기각하여 올바른 결정을 할 수 있는 확률)
    • 계산법 : $$ 1-\beta$$ (2종 오류를 범하지 않을 확률)
    • 차이 or 효과가 있는것을 통계적으로 차이 or 효과가 있다고 보여 주는것
  • 통계기법마다 검정력이 서로 다름
  • 검정력에 영햐을 미치는 요소
    1. 표본 크기($$n$$) : 다른 조건들이 같다면 포본 크기가 클수록 검정력은 커진다
    2. 유의수준($$\alpha$$) : 유의 수준이 높을수록 검정력이 커진다.
    3. 검정되는 모수의 참값:참값과 귀무가설에서 명시된 값의 차이가 클수록 검정력이 커진다.

      연구자들은 제 1종 오류를 5%로 유지하면서 검정력을 최대화하는 통계 기법을 사용하고자 함

중요 시간 가지고 다시

6.4 무작위화

  • 선택될 확률이 동일함을 의미

  • 7. 직교 설계와 비 직교 설계

  • 직교(orthogonal) 설계 : Missing 데이터가 없다

  • 비직교(non-orthogonal) 설계 : Missing 데이터가 있다 --> 비 직교 데이터에서는 순서가 중요

8. Aliasing(앨리어싱) :

  • 모형의 결과 중 하나 또는 그 이상의 행에서 예사외로 NA가 나타나는 것
  • 모수 추정치에 대한 정보가 없을 때 발생
  • 종류
    • 내적 에일리어싱 : 모형의 구조에 따라 발생
    • 외적 에이리어싱 : 데이터의 속성에 따라 발생

중심 극한 정리(Central limit theorem)

  • (데이터 자체는 어떤 중심 값 주변으로 모이는 경향이 없더라도) 반복적 실험에 의해 계산된 값들은 중김 값 주변에 모이는 경향이 있다.
  • 표본의 크기가 충분히 크다면 표본 변수들의 그 합 또는 평균의 히스토 그램은 정규분포 곡선에 수렴한다.

많은 통계 모형들은 자료가 정규 분포라는 가정에 기초 하여 시행한다. 데이터가 충분히 크다면 중심 극한 정리에 의하여 정규분포라고 가정하고 통계 분석을 할 수 있다.

Correlation coefficients

Continuous vs. Continuous

  • cor(x, use, method = “Pearson OR spearman OR kendall”)
    • Pearson : quantitative variables 간의 degree of linear relationship
    • Spearman’s : rank-ordered variables. 간의 degree of relationship
    • Kendall’s Tau : nonparametric measure of rank correlation
  • cor.test() :

Continuous vs. Nominal

  • Significance tests: run an ANOVA. In R, you can use ?aov.
  • Effect size (strength of association): intraclass correlation, ?icc

Nominal vs. Nominal

  • Significance tests: run a chi-squared test. In R, you use ?chisq.test.
  • Effect size (strength of association): calculate Cramer's V. In R, you can use ?assocstats in the vcd package.
  • 명목형 && 이분변수 : 크래머(Cramer’s phi)

http://stats.stackexchange.com/questions/108007/correlations-with-categorical-variables http://stats.stackexchange.com/questions/119835/correlation-between-a-nominal-iv-and-a-continuous-dv-variable/124618#124618

---

*[AM]: Arithmetic Mean

*[GM]: Geometric Mean

*[HM]: Harmonic Mean

1. 테스트 ↩

1 : https://en.wiktionary.org/wiki/Appendix:Unicode/Mathematical_Operators "Appendix:Unicode/Mathematical Operators"

2. SD = Standard Deviation ↩

results matching ""

    No results matching ""