슬라이드 한장으로 보는 backprop : 김성훈 교수 작성
Backpropagation
공식 유도 자료: 딥러닝 제대로 시작하기 4장 (미분 공부 후 다시)
How Can we learn $$w1, w2, b1, b2$$ from training data
Layer가 깊어 질수록 초기의 weight와 Bias를 찾기 힘들다 (Marvin Minsky,1969)
- Backpropagation으로 가능 (Paul1974, Hilton1986)
미분 chain rule 활용
- $$ f(x) = wx + b$$를 도식화 한
- 각 값이 $$f$$에 미치는 영향 구하기
1. 방법 A: Forward
- 각 값을 사용 ($$w= -2, x=5, b=3$$)
- f = -7 계산
2. 방법 B : Backward
- 기본 $$ f(x) = wx + b $$에서 미분, 편미분 통하여 값 도출
- $$ g= wx $$ 치환 하면 $$f(x) = g + b$$
위 치환 식 $$ g= wx $$ 에서
- w를 기준으로 g를 편미분하면 $$ \frac{\partial g}{\partial w} = x$$ (w는 1이되고, x는 상수이니 $$1*x = x$$)
- x를 기준으로 g를 편미분하면 $$ \frac{\partial g}{\partial x} = w $$
위 치환 식 $$f(x) = g + b$$ 에서
- $$ \frac{\partial f}{\partial g} = 1$$
- $$ \frac{\partial f}{\partial b} = 1$$
위 도출된 값 4개만을 활용하여 값을 구할수 있음
Step 1. 이미 알고 있는 * $$ \frac{\partial f}{\partial g} , \frac{\partial f}{\partial b} $$ 값 1 입력
Step 2. 모르는 $$\frac{\partial f}{\partial w} , \frac{\partial f}{\partial x} $$ 는 g를 사용하는 복합함수 확인,chain Rule 사용
- $$ \frac{\partial f}{\partial w} $$를 chain Rule 사용 변환 $$ = \frac{\partial f}{\partial g} \frac{\partial g}{\partial w} = 1 x = 1* 5 = 5$$ (w가 1만큼 변하면 f는 5만큼 영향)
- $$ \frac{\partial f}{\partial x} $$를 chain Rule 사용 변환 $$ = \frac{\partial f}{\partial g} \frac{\partial g}{\partial x} = 1 -2 = -2$$ (x가 1만큼 변하면 f는 -2만큼 영향)
- A Step by Step Backpropagation Example
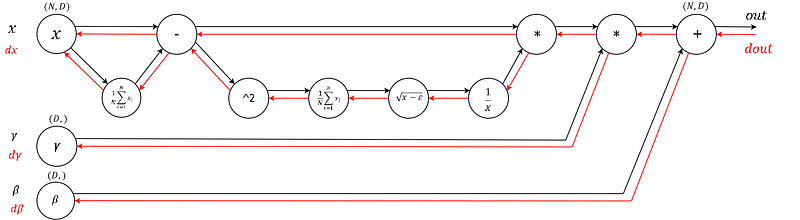
- Understanding the backward pass through Batch Normalization Layer
- This tutorial teaches backpropagation via a very simple toy example
- CNN 역전파를 이해하는 가장 쉬운 방법 : 2017년 1월 23일 조준우 작성글
- Yes you should understand backprop
- Backpropagation 설명 예제와 함께 완전히 이해하기: Jaejun Yoo블로그
- A Derivation of Backpropagation in Matrix Form
- 라온 블로그_Backpropagation for Neural Network(역전파): Class 8, Class 9