1. 개요
1.1 역사
- 2013년 Atari BreakoutGame에 적용하면서 인기
- 2015년 human level control
- 2016년 AphaGo
2. Q-Learning (for deterministic world)
Q(state, Action)을 이용한 문제 해결
- $$ Max_a {Q(S_1,a)} = Q가 a를 바꿈으로써 얻을수 있는 최대값 $$
- $$ argMax_a{(S_1,a)} = Q가 최대값이 되게 하는 변수 a의 값 $$
2.1 기본 알고리즘
- $$ Q(S,a) = r + Max_{a^1}Q(S^1, a^1) $$
2.2 기본 알고리즘 + E&E
E&E(Exploit-현재값 이용 & Exploration-탐험적 도전찾음)
- Dummy Q-Learning의
Select an Action "a" and execute it의 a방법 - 새로운 길을 찾는 기능 추가
- ex: 맛집 찾기, 평일은 아는곳(Exploit), 주말은 새로운 곳(Exploration)
구현 방법 1 : E-greedy
e=0.1 # 10%의 새로운곳 가기- 랜덤값을 뽑아서 e보다 작으면 새로운곳, e보다 크면 가던곳
구현 방법 2 : Decaying E-greedy
e= 0.1 / (i+1) # for i in range (1000)- 학습 초기에는 랜덤 비율이 높게, 학습 후반으로 갈수록 랜덤 비율이 작게
구현 방법 3 : Add random noise
a=argmax(Q(s,a) + random_values)
구현 방법 4 : Add random noise with decaying
a=argmax(Q(s,a) + random_values/(i+1)) # for i in range (1000)
E-greedy방식 대비 Random의 장점은 앞의 Q(s,a)의 값이 고려 되어 선택이 가능
2.2 기본 알고리즘 + E&E + Discount Future Reward
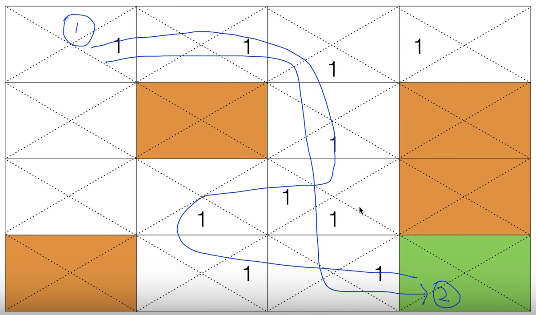현재 방법은 위 그림 중 (1)과 (2)중 어느것이 좋은줄 판단 어려움 (2가 좋음)
구현 방법 : Discount Future Reward
- 현재 받는것은 값을 크게 받고, 이후에 받는같은 $$\gamma$$을 곱해서 받고, 그 이후는 $$\gamma$$의 $$\gamma$$을 곱해서 받음
- $$ Q(S,a) = r + \gamma * Max_{a^1}Q(S^1, a^1) $$
김성훈 교수 설명 Youtube
3. Q-Learning for Non-deterministic(=Stochastic) world
미끄러운 얼음판 처럼 목적대로 움직이지 않는 경우
3.1 기본 알고리즘 + Learning rate
Q의 의견은 참조(=Learning rate,$$\alpha$$)만 하고, 내가 가고 싶은 방향($$1-\alpha$$)으로 간다.
$$ Q(S,a) = (1-\alpha) Q(S,a) + \alpha [r + Max_{a^1}Q(S^1, a^1)] $$
4. Q-Network
- Q-learning의 경우 Table형태의 작은 배열크기는 가능하지만, 픽셀을 인지하여 겜임을 하는 경우는 크기가 커져 사용이 어려움
- Q -Network를 이용하여 해결 가능 - 딥마인드의 Atari게임 핵심 알고리즘
Reinforcement Learning + Deep Learning 방식
4.1 네트워크 모델 1
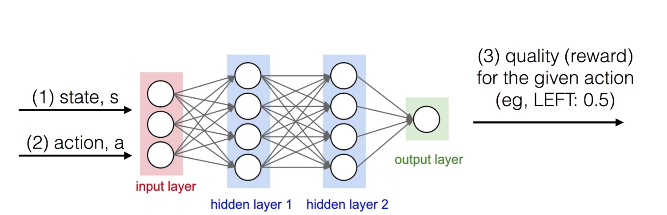
- S 와 a를 주고 맞는 Q Value를 도출
4.3 네트워크 모델 2
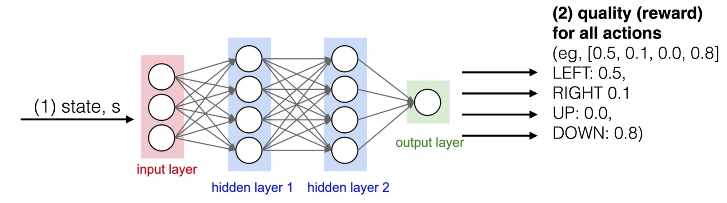
S를 주고 a에 따른 Q value를 도출
Linear Regression의 방식과 비슷 ,Cost함수만 변경 $$ Cost(w) = (Ws-y)^2 $$일때 $$ y= r + \gamma maxQ(s`) $$
Q Network는 Convergence가 안되고 Diverges(학습이 안됨)됨<-무슨말인지 ??
- 이유 1 : Correlation between samples
- 이유 2 : Non-Stationary Targets
이를 해결한 알고리즘이 DQN임
- Tensorflow Q network 코드 설명 [Youtube]
5. DQN
- DQN Paper : www.nature.com/articles/nature14236
- DQN Code : sites.google.com/a/deepmind.com/dqn
5.1 기본 방식의 문제점 및 해결책
A. Correlation between samples
- 입력으로 활용되는 환경(샘플)들이 상당히 유사하다. Correlation이 크다.
해결책 : Capture and replay로 해결(일명,Experience replay)
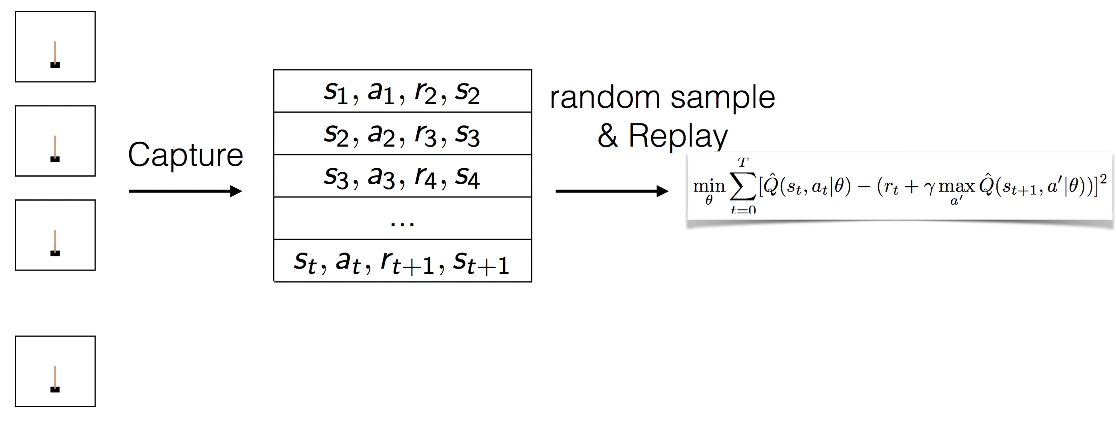
- Action을 수행하고 이에 대한 결과값 S,R들을 바로 학습에 사용하지 않고 버퍼에 보관
- 보관된 버퍼의 값중 일부를 Random하게 선택하여 학습 수행
B. Non-Stationary Targets
Target이 움직임
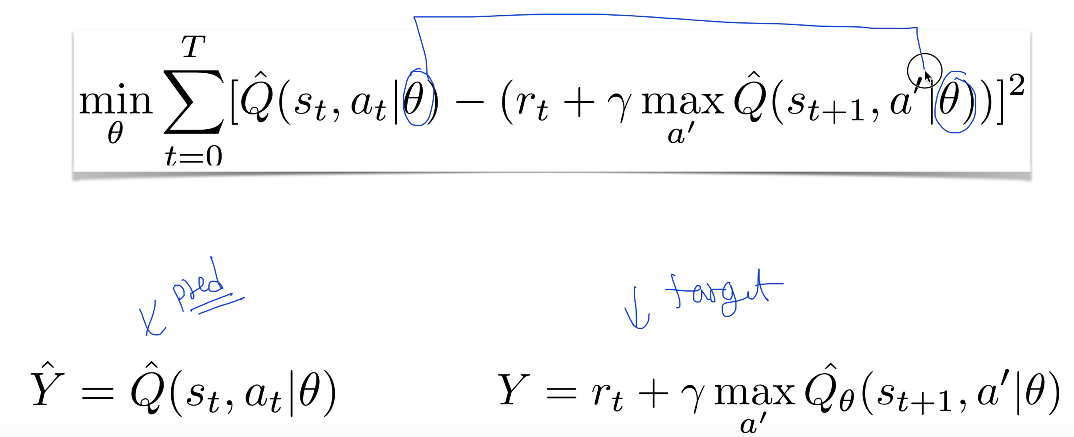
- Q-Net의 기본 알고리즘의 목적은 예측($$\hat{Y}$$)과의 값을 최소화 하는것임 target($$Y$$)
- 문제는 각 알고리즘에서 쓰인(업데이트하는) $$\theta$$가 양쪽에서 모두 쓰임
- 즉, 화살을 쏘는데 과녁판이 움직이는 것과 같음
해결책 : Separate Networks: Create a target network
- 네트워크를 하나 더 만듬
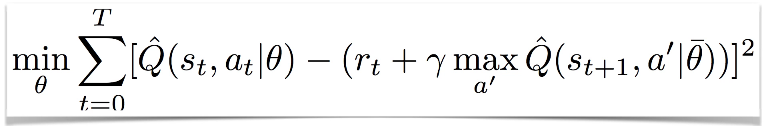
- 기존 공식의 $$\theta$$를 양쪽에서 쓰는것이 아닌, 새로운 $$\overline{\theta}$$를 사용
- 두개가 서로 다른 네트워크임