Sensor Fusion

예제 코드 : Implementation - snippet - kalmanFilter-basic-code 참고 (Sensor Fusion — Part 2: Kalman Filter Code)

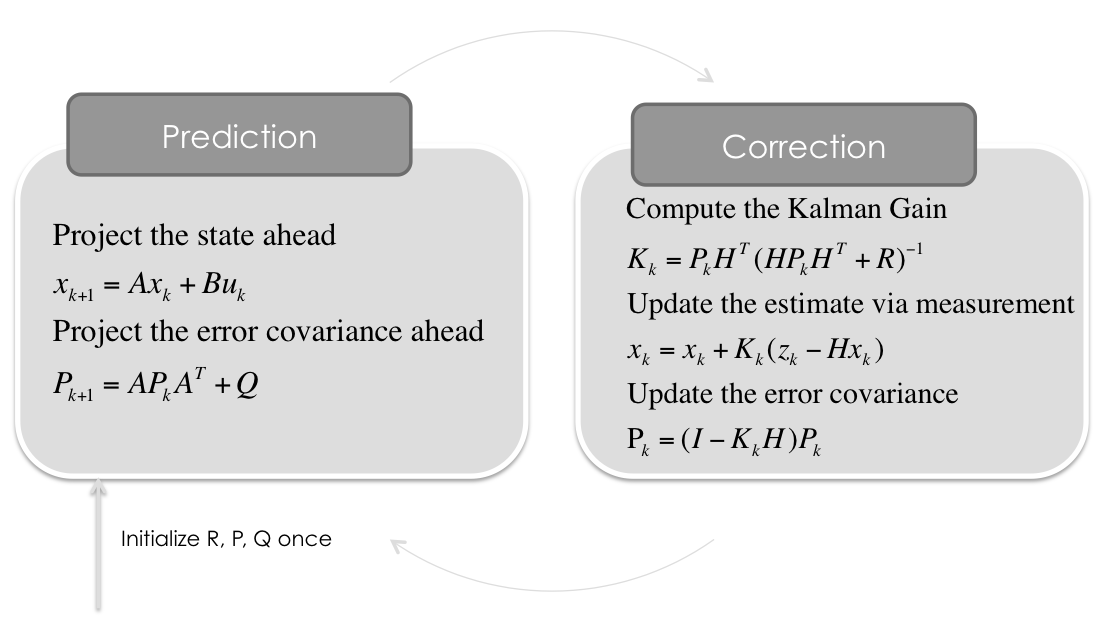
1. Kalman Filter basics

내용 : 칼만필터 기반 차량 추적 및 센서 퓨전 I will try to explain Kalman filter algorithm along with an implementation example of tracking a vehicle with help of multiple sensor inputs, often termed as Sensor Fusion.

기본 3가지 구성 요소 Kalman filter in its most basic form consists of 3 steps.

Predict — Based on previous knowledge of a vehicle position and kinematic equations, we predict what should be the position of vehicle after time t+1.
Measurement — Get readings from sensor regarding position of vehicle and compare it with Prediction
Update — Update our knowledge about position (or state) of vehicle based on our prediction and sensor readings.

여러 변형들 All variants of Kalman filter are just different variants of above 3 steps, depending upon

different Kinematic equations you want to use and
different kind of sensor reading which you want to incorporate in algorithm.

1.1 Predict

A. Input & kinematic equations

기본적 속도, 거리, 시간 정보로 공식 세움 Using basic equations of velocity, distance and time, we know that if position of my vehicle at time t is at x location, then at time t+1 the vehicle will be at location x + ((t + 1) — t) * v, where v is velocity of vehicle.
가속도 정보를 알고 있으면 이를 고려함 Digging in further, if we have acceleration value available with us, we can add it to above equation and update new position of vehicle to x + ((t + 1) — t) * v + 0.5 * a * ((t + 1) — t)2.

공식 : Formalizing above equations, lets denote current state of vehicle,

which consists of its current location and velocity as a vector x.
So vector x will have 4 elements,
- namely px, py, vx, vy;
- representing position and velocity in x and y directions respectively.

예시를 간소화 하기 위해 2D(x,y)로 한정한다. The positional x and y distances are with respect to our vehicle’s own position. So if we say a vehicle is at position px and py, we mean that it is at a distance of px and py from our vehicle.

Moving on, let’ define velocity and acceleration as velocity and acceleration vectors having velocity and acceleration data in x and y direction respectively. We will denote change in time as delta_t.

With this, our individual equations for tracking position and velocity becomes:

Px(t+1) = Px + delta_t vx + 0.5 ax * delta_t 2
Py(t+1) = Py + delta_t vy + 0.5 ay * delta_t 2
Vx(t+1) = Vx + ax * delta_t
Vy(t+1) = Vy + ay * delta_t

매트릭스 연산이 성능에 더 좋다. Without going into details, one thing we should understand is that performing matrix operation is much more computationally effective than solving individual equation.

A simple justification being, if we consider above 4 equations, a controller will need to perform following actions 4 times.

i) Create a variable Px(t+ 1),
ii). get value of Px
iii). get value of delta_t
iv). get value of vx
v). get value of ax
vi). perform mathematical operations
vii). store result.

All these operations will have to be performed one time each for each equation.

Coming back to 1s and 0s, lets convert our 4 individual equations into following matrix form.

So now our 4 equation gets clubbed together and they look like this.

x_new = A * x + B * u


A = [
    [1, 0, Δt, 0],
    [0, 1, 0, Δt],
    [0, 0, 1, 0],
    [0, 0, 0, 1]
    ]

B = [
    [0.5 * Δt * Δt, 0],
    [0, 0.5*Δt * Δt],
    [Δt, 0],
    [0, Δt]
    ]

첫행 : Taking first row from above matrix equation

px_new = [(1 px) + (0 py) + (delta_t vx) + (0 vy) ] + [ (0.5 delta_t delta_t acceleration_x) + (0 acceleration_y) ]
px_new = px + delta_t vx + 0.5 acceleration_x * delta_t 2

which is same as one we had come up with before converting individual equations to matrix form.

Here matrix A and B are just matrices representing kinematic equations for position, velocity and acceleration.

B. State Covariance Matrix P (불확실)

컴퓨터에도 불확실성은 존재 This uncertainty factor holds true for computers too.
칼만필터의 특별한 점 A thought might have entered your mind saying, so what’s so great about Kalman filter, above mentioned kinematic equations been known for decade, we can use it in matrix form if you like it and start predicting.
차량의 위치 예측시 불확실성도 같이 간주 해야 함 So when we are asking computer to predict the value of our new state of vehicle, we need to ask it about its uncertainty too.
In Kalman filter language this uncertainty is represented as covariance matric.

칼만 필터에서 불확실성은 covariance matric로 표현 된다.

Lets denote our State Covariance Matrix as

P = [variance_px, 0, 0, 0],
    [0, variance_py, 0, 0],
    [0, 0, variance_vx, 0],
    [0, 0, 0, variance_vy]
    """
    variance_px = uncertainty in predicted x position
    variance_py = uncertainty in predicted y position 
    variance_vx = uncertainty in predicted x velocity 
    variance_vy = uncertainty in predicted y velocity  
    """

0의 의미 : 서로 비의존적이다. All the remaining 0 terms are to say that uncertainty in one value is independent of other value, meaning to say my position x uncertainty is nothing to do with my uncertainty in y direction.

항상 비 의존적이지는 않지만 간소화를 의해 본 예시에서는 0으로 처리 This need not be true in every case. In some case the variables you are tracking may actually depend on each other. But we will use the simplistic approach here and make other values as 0.

This actually makes it a ‘variance’ matrix, but covariance is much more widely used term.

C. Noise Covariance matrix Q

공식이 복작해 지긴 하지만 Noise Covariance matrix Q도 포함 해야 한다. At the risk of making our equations a bit complex, I want to introduce Process Noise Covariance matrix Q.

계산시 노이즈를 고려 해야함 In any covariance matrix calculations (which is matrix P in our case), you can have a certain amount of noise which needs to be added into it to come up with a new predicted covariance in the estimation.

칼만 필터는 순환프로세스 이기에 매 센서 정보 수신시 covariance matrix와 함께 predict를 수행 해야 한다. As Kalman filtering is a continuously iterative process, we need to keep predicting the state vector along with its covariance matrix every time we have a new reading from sensor,

so that we can compare the predicted value (step a) with sensor value (step b) and
update our information about the vehicle we are tracking (step c).

우리는 이미 updating state vector 공식은 알고 있으며 update covariance matrix 공식은 아래와 같다. We already have equations for updating state vector, and the equation to update covariance matrix is as given below.

updating State_vector: x = A * x + B * u
update Covariance_matrix: P = A * P * AT * Q

1.2 Measurement

모든 시작은 센서 정보 수신 부터다

Now let’s say we receive a sensor reading for the position of the vehicle we are tracking.
Actually the sequence of operation is, we trigger Kalman filter calculation only when we receive sensor readings.
The sensor reading will usually have a timestamp associated with each reading.

We read that timestamp, calculate difference between timestamp of last reading and this one.

Perform prediction as per above explanation using delta_t = timestamp difference between two readings and
then come to Measurement and update part for sensor input.

Lidar센서는 위치 정보는 있지만 속도 정보는 없다. Commonly use sensors like Lidar and Time of flight sensors will give you readings regarding position of a vehicle, but not its velocity.

So our sensor reading will be of form vector z = [px, py].

STEP A단계에서 이 측정값(z)과 예측값(x)을 비교 한다. As stated before, we need to compare this measurement value with the value predicted in step a.

그러나 이 두값은 different order이다. But looking at both vectors (predicted state vector x and measurement vector z), we see that both are of different order.

‘x’ matrix = 4 x 1 (속도 정보 포함)
‘z’ matrix = 2 x 1

따라서, state matrix(x??)를 z와 같은 크기로 변환 하기 위해 H Matrix가 필요하다. Hence to convert state matrix to same size as z, we introduce matrix “H”.

매트릭스 연산의 기초에 따라 matrix H는 2 x 4 이다. Getting into matrices basics, to convert a 4 x 1 ‘x’ matrix to 2 x 1 ‘z’ matrix (while keeping top two values as it is and removing velocity variables) we use a 2 x 4 matrix H.

비교 공식 : So the equation comparing predicted value with measurement becomes

$$y = z - Hx$$,

결과로 다름정도 출력 which gives us the difference between both values.

kalman gain 계산

Well, in this step, we will also be calculating Kalman gain.

Gain Factor는 차량 state의 final value를 결정하는데 사용된다. This gain factor is basically used to decide final value for vehicle state

예측값과 측정값 사이에서 선택 된다. ,choosing an appropriate value between predicted and measurement one’s.

이미 예측값의 불확실성은 State Covariance matrix P라는것은 알고 있다. We have already seen uncertainty in predicted value as State Covariance matrix P.

측적값의 불확식성은 Measurement Covariance matrix R이다. The corresponding uncertainty matrix for measurement readings is Measurement Covariance matrix, denoted with letter R.

Our state variable was having 4 variables (x, y position and velocity) so its covariance matrix was a 4 x 4 matrix.

Lidar센서는 위치 정보 x,y만 알수 있다. 따라서 Measurement Covariance Matrix는 2x2이다. As stated before, lets consider that our sensor just gives us positional reading in x and y directions. In that case our Measurement Covariance Matrix will be of 2 x 2 shape as shown below.

R = [ 
    [variance_in_pos_x_reading, 0]
    [0, variance_in_pos_y_reading]

칼만게인에서는 예측과 측정 방법의 불확실성을 비교한다. 비교 방법은 전체 불확실성에서 예측값의 불확실성 퍼센트로 계산한다. In Kalman gain value, we compare uncertainty in predict and measurement methods by calculating percentage of uncertainty in predicted value to that of total uncertainty.

In other words

Kalman Gain = \frac{Uncertainty_in_predicted_state}{(Uncertainty_in_predicted_state + Uncertainty_in_measurement_readings)}

We know

uncertainty in predicted state is matrix P and
that in measured value is matrix R.

크기 변환 H matrix But as you can see, both of them are of different size. Hence we use H matrix to convert P matrix to correct size.

최종 칼만 게인 공식 With that the Kalman Gain equation becomes

$$ K = \frac{( P HT )}{( ( H P * HT ) + R )}

H Matrix required to calculate Kalman Gain with a 4 x 4 P Matrix and 2 x 2 R matrix will be as shown below

H = [ 
    [1, 0, 0, 0],
    [0, 1, 0, 0]
    ]

P매트리스에 H매트리스를 덧붙이는건 매트릭스 연산때문이다. Again, the padding of H matrix around P matrix is only for matrix operation, please don’t let it scare you.

칼만게인은 단순한 퍼센트 구하는 공식이다. Kalman gain is just a simple percentage formula.

아래의 모든것이 준비 되었다. Well, with predicted value, measure value and Kalman gain values in hand, its time to move to update state, where we make final update to state vector x and its corresponding covariance matrix P.

predicted value,
measure value
Kalman gain values

이제 update state를 진행 할수 있다. 이 단계에서 마지막으로 state vector x 와 covariance matrix P를 업데이트 한다.

1.3 Update

final state vector : $$ x = x + Ky. $$

# 예측값이 정확할때 
Imagine we are very confident in our predicted value, then our covariance P will have very small variance values. 

This in turn will make Kalman Gain ( which is Uncertainity in predicted state / Uncertainity in predicted state + Uncertainity in measurement readings.) a small number as final equation will be of form small number / (small number + big number). 

In this case, if we consider final x equation, we take our predicted value and just add a small portion of it’s difference (that is, difference between predicted and measured values) to measured value. 

Because Kalman gain will be a small value as per above theory, equation of x will be of form; x = x + (small number * y)

As you can see, this will cause final x to lean more towards predicted value, which is in line with starting assumption we made that we have high confidence in predicted value compared to measured value.

Similarly, the equation to update covariance matrix is

$$ P = (I-KH) P.

Again, H matrix is used for matrix manipulations.

최종 공식 And with that we have all the tools required to implement a complete Kalman Filter with following equations

A. Predict	B. Measurement	C. Update
$$ X = A X + B u $$ $$ P = A P AT * Q $$	$$ Y = Z — H X $$ $$ K = ( P HT ) / ( ( H P HT ) + R ) $$	$$ X = X + K Y $$ $$ P = ( I — K H ) * P $$

Kalman Filter basics