The Geometry of Linear Equations

0. 용어 정리

0.1 선형

‘선형(Linear)’이란 ‘줄 선(線)’ + ‘모형 형(型)’이 결합한 단어로, 선의 형상을 갖는 것입니다.

선형성

wiki : 그래픽적으로 직선 형태로 표현될 수 있는 수학적 관계(또는 함수)를 의미
통계: 독립 변수에 대한 결과가 1차식으로 표현될 것
통계: 독립 변수에 대한 결과가 1차식으로 표현될 것
기계: 수학적으로 변수를 x,y, 상수를 a,b라 할 때 y=ax+b가 만족할 때

어떤 시스템에서 입력에 대응하는 출력이 나온다는 의미, ‘원인(입력)과 효과(결과)간의 비례(직선) 특성’

선형성을 가진다 = 예측이 가능하다

0.2 대수

‘대수(algebra)’란 대신할 대(代) + 셈수(數)가 결합한 것, 수를 대신하여 문자나 수학법칙으로 표현하는 것

y = 3x 에서 대수는 x,y /3는 계수

대수 = 산수

0.3 선형 대수

선형 방정식을 풀기 위한 방법론
선형성을 가지는 대수로 이루어진 방정식들의 해를 구하는 방법론
선의 형상을 가진 것을 수가 아닌 문자나 수학법칙으로 표현해야 것
선형대수는 어떤 함수(Function, Mapping Operator, Transformation)가 선형 함수(Linear Function)일 때 그 성질을 배우는 것
선형 대수는 벡터(Vector)와 행렬(Matrix)을 이용하여 표현되며, 대표적인 선형 함수로는
- 정비례 함수(y=ax)
- 미분
- 적분
벡터(Vector)와 행렬(Matrix)를 배우는 학문

[참고] 백터와 행렬을 이용한 산수/산수와의 유사성

수의 닫힘 집합 = 벡터 공간
절대값 = 행렬값(Determinant)
양수 = 양정치(Positive-definite Matrix)

[참고] 선형대수학과 머신러닝

머신러닝 = 데이터를 처리 = 방정식을 풀어 해를 구한다 = 방정식을 푸는 방법이 선형대수

1. 선형성 정의

행렬 연산을 하려면 선형성을 만족 해야 함.

선형성 요구 사항

Superposition : $$f(x_1 + x_2) = f(x_1) + f(x_2) $$
Homogeniety : $$ f(ax) = a f(x) $$

합쳐서 $$ f(a_1 x_1 + a_2 x_2) = a_1 f(x_1) + a_2 f(x_2) $$

원점을 지나는 평면상의 직선은 선형성을 만족 하며, 백터라고 부름

Matrix Form

$$ \Rightarrow \begin{bmatrix} 2 & -1 \ -1 & 2 \end{bmatrix} \begin{bmatrix} x \ y \end{bmatrix} = \begin{bmatrix} 0 \ 3 \end{bmatrix}

2. 선형 시스템 해석 하는 방법

2.1 Row picture

방정식이 나타내는 기하(Geometry) 들의 교차(Intersection) 가 $$A\mathbf{x} = \mathbf{b}$$ 의 solution 이 된다. 예를 들어 A 가$$ 2\times2$$ 행렬이면 두 직선의 교차를, $$3\times3 $$행렬이라면 세 평면의 교차를 나타낸다. 1

2.2 Column picture

$$\mathbf{x}$$ 는 A 의 열 벡터들의 선형 결합 계수다. 다시 말해 A 의 열 벡터들의 선형결합으로 $$\mathbf{b}$$ 를 나타낼 수 있다면 해가 존재한다. $$\mathbf{b}$$ 에 도달하기 위해 A 의 열 벡터들을 늘이거나 줄이는 그림을 상상해보자.

Row picture	column picture
row 방법 = 내적(Dot Product)	Column 방법 = 선형결합(Linear Comnibation)
$$ 2x - y = 0 $$ $$ -x + 2y = 3 $$	$$ x\begin{bmatrix} 2 \ -1\end{bmatrix} + y\begin{bmatrix} -1 \ 2 \end{bmatrix} = \begin{bmatrix} 0 \ 3 \end{bmatrix} $$

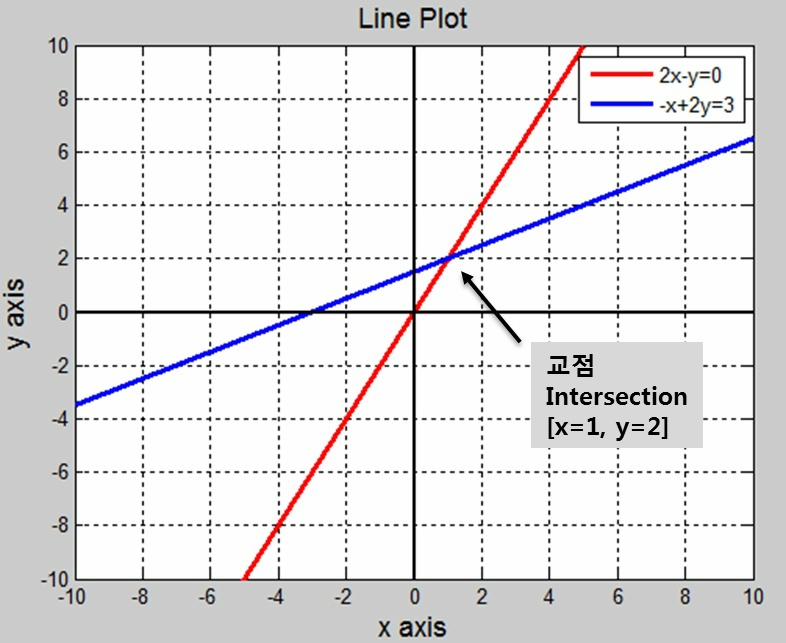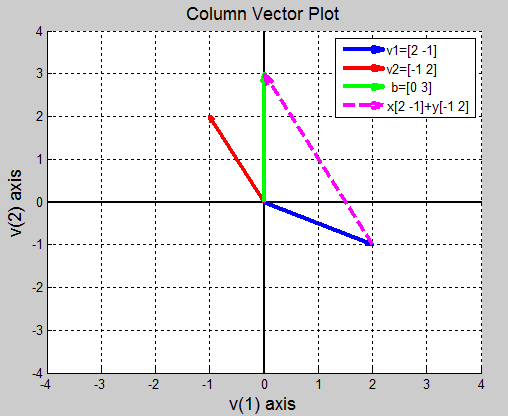교점을 찾는것이 목표	벡터 v1과 v2에 얼마의 상수 x, y를 각각 곱하여 벡터 b를 만드는 것

01 The Geometry of Linear Equations