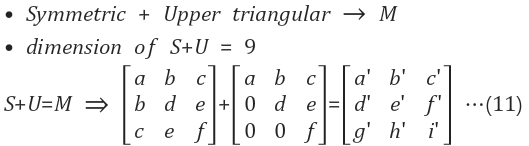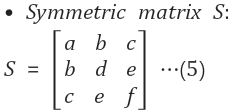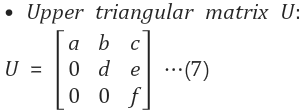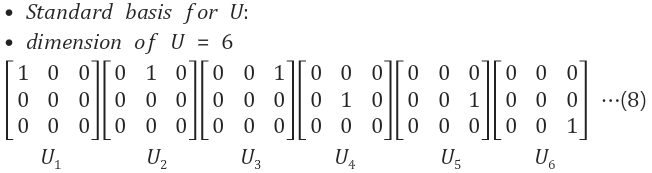행렬 공간(Matrix spaces, M)

• 일종의 새로운 백터 공간(vector Space) = 3x3크기의 모든 정방행렬(square matrix)
  • 벡터공간 조건 만족: 선형 결합(Linear combination)을 해도 같은 공간에 위치

1. 행렬공간의 Subspace

M의 차원이 9이므로 M의 기저 역시 9개가 될 것이다. M의 기저는 아래와 같다.

특히 이렇게 1과 0으로만 구성된 기저를 Standard basis라 한다

1.1 3x3 대칭행렬(Symmetric Matrix, S)

정의 : 대각선을 기준으로 아래 & 위의 원소들이 같은것

9개의 M기저 중 S에 포함되는것은 6개- 차원이 6개

1.2 3x3 상삼각행렬(Upper triangular Matrix, U)

정의 : 대각선을 기준으로 위쪽에만 원소들이 있는것

9개의 M기저 중 U에 포함되는것은 6개 - 차원이 6개

1.3 3x3 대각 행렬(Diagonal Matrix,D)

정의 : 위에서 살펴봤던 두 개의 부분 공간 행렬의 조합

A 교집합 조합

9개의 M기저 중 D에 포함되는것은 3개 - 차원이 3개

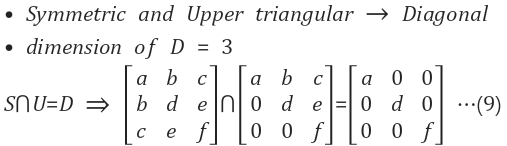
B. 합집합 조합

이 둘은 다른 방향으로 존재한다. 따라서 애초에 이 둘을 함께 놓을 수가 없다. 따라서 이 합집합은 부분 공간이 아니다

C. 더하기 조합

대칭행렬과 상삼각행렬의 조합을 통해 모든 3x3 크기의 모든 행렬 M을 만들 수 있다 - 차원이93개