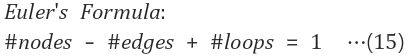선형 대수의 응용

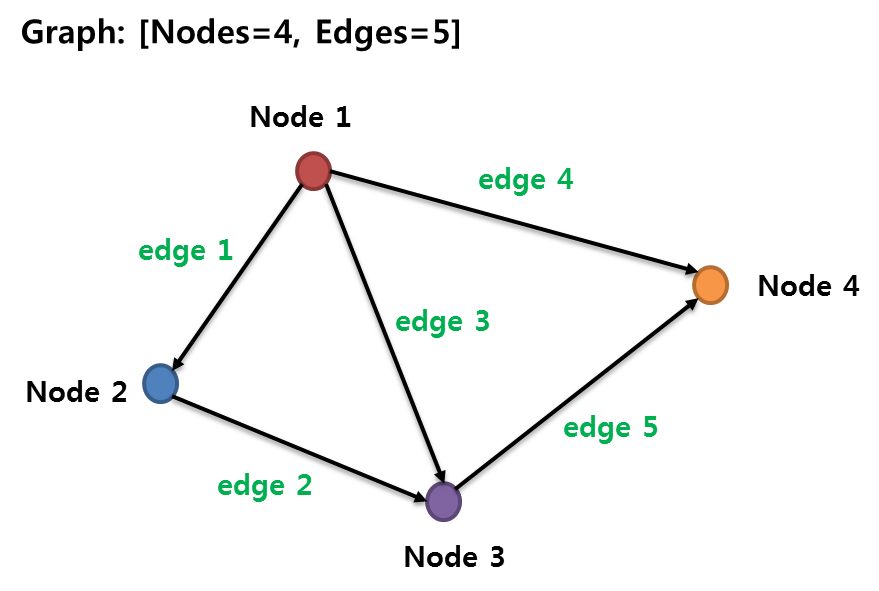
응용 1 : 그래프(Graph)

어떤 객체(object=Node)들과 그들을 연결짓는 선(Line=Edge)을 통해 그들 사이의 관계를 나타내는 구조

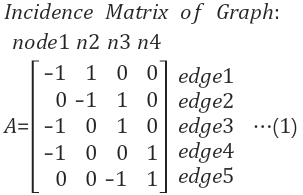
1. 근접행렬(Incidence Matrix)

그래프의 노드와 그들의 연결관계를 행렬(Matrix)로 나타낸것

규칙 : 출발점은 -1, 끝점은 1

  • edge 1 : Node1 = -1, Node2 = 1, 나머지는 = 0
  • edge 2 : Node2 = -1, Node3 = 1, 나머지는 = 0
  • edge 3 : Node1 = -1, Node3 = 1, 나머지는 = 0

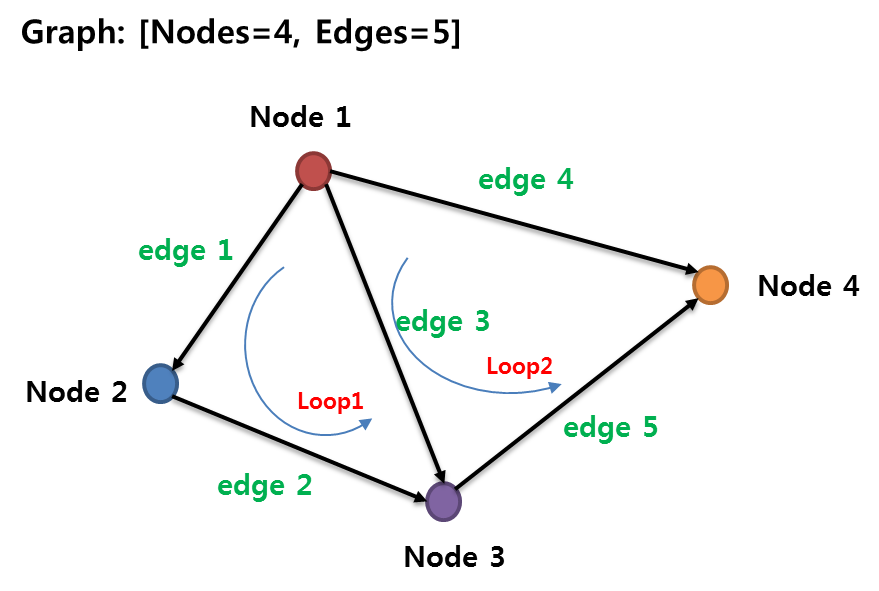
2. Loop

node들이 연결되어져 있는 부분 그래프(subgraph)

  • edge1, 2, 3에서 loop1
  • edge3, 4, 5에서 loop2
  • edge1, 2, 4, 5에서 loop3

3. 근접 행렬 + Loop

어떤 그래프의 loop에 대한 Incident matrix의 row들은 선형종속(linearly dependent)의 특성을 갖는다는 것

  • edge1,2,3= loop1이다.
  • A의 row1, 2, 3에 해당하는 것
  • loop1의 row들은 종속(dependent)이다 = row1과 row2를 더했을 때 row3이 나옴

4. 정리

  • 어떤 그래프에서 loop의 개수는 edge의 개수에서 node의 개수-1과 같다.

    • 여기서 nodes-1은 rank를 의미하는데, 그래프의 Incidence matrix에서 항상 rank=n-1이기 때문이다. n은 column의 개수이고 1개의 column은 종속이므로 1을 빼주면 rank(=dimension)가 된다.

  • edge의 수는 Incidence matrix에서 row의 수와 같다.

    • 즉 #edge=m이다.

결국 이 식이 의미하는 것은 어떤 그래프에서 독립적인 loop의 개수는 그래프의 Incidence matrix의 left null space와 같다

사실 이 공식을 약간 다르게 쓰면 오일러의 공식(Euler's Formula)이 된다.

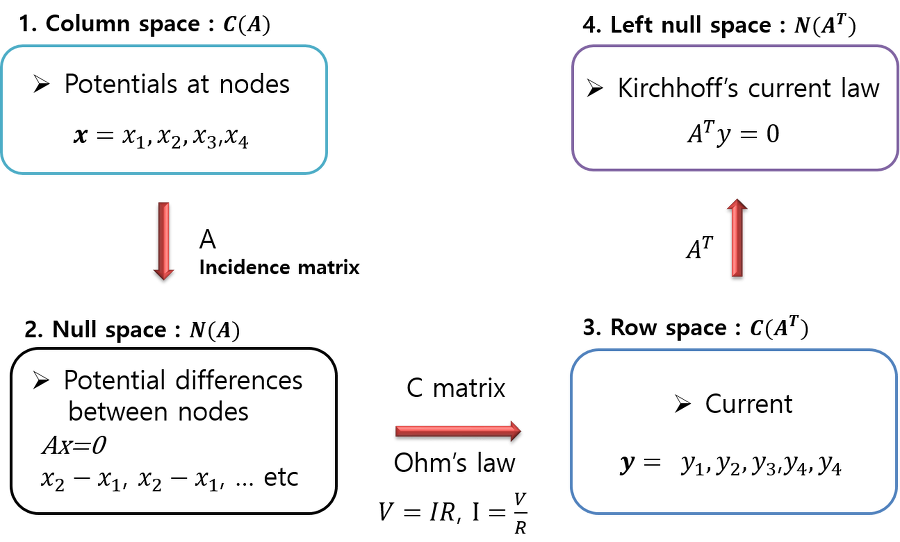
5. 그래프 모델과 선형대수의 부분 공간과의 관계도

응용 2: 전자회로의 그래프 모델링

Skip

results matching ""

    No results matching ""