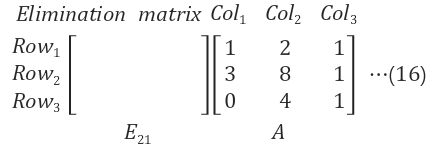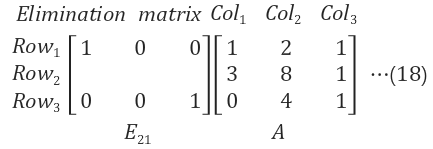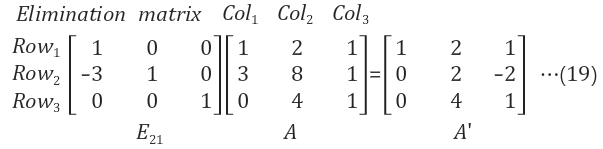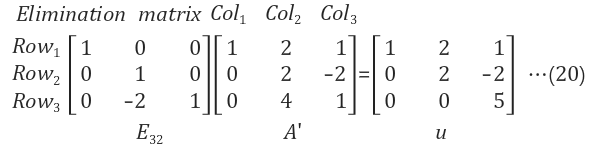가우스 소거법

해를 구하기 위한 방법

1. 가우스 소거법 + 후방 대입법
2. 소거 행렬 + 행렬 곱셈

1. 가우스 소거법 $$\rightarrow$$ 후방 대입법

1.1 가우스 소거법

• 개요 : 연립 방정식을 푸는 방법
• 요구사항 : 미지수의 갯수와 방정식의 갯수가 같은 경우
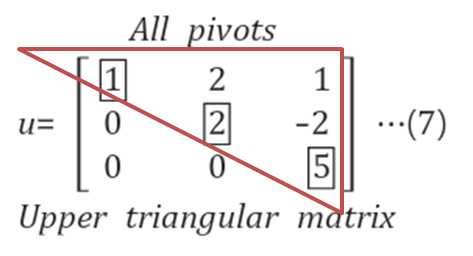
• 목적 : 시스템 행렬 A를 upper triangular matrix로 만드는것
• 방법 : 기준이 되는 식에 적당한 상수를 곱하고, 제거하고자 하는 항이 있는 식에서 이를 빼준다.
  • 왼쪽에서 오른쪽, 위에서 아래 방향으로

All pivots are non-zero -> G.E has a unique solution

고려 사항 : 피봇에 0이 존재 하면 가우스 소거법 사용 못함

• pivot에 0이 존재 하여 가우스 소거법을 사용 못할경우, 순서를 바꾸어 문제 해결 --> pivoting

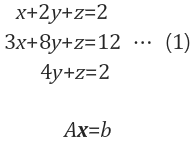원식	소거후 U행렬

2.2 Back-substitution (후방 대입법)

기존 소거법은 Ax = b에서 A만을 소거 하는 방식, b까지 고려 하여 소거법을 적용 해야 한다

1. 일단 b까지 추가 하여 행렬을 생성 = augmented Matrix

2. 생성된 행렬을 가우스 소거법 실시

$$ x + 2y + z = 2 $$

$$ 2y -2z = 6 $$

$$ 5z =-10 $$

3. 후방 대입

즉 z텀(z=-2)만 남아있는 세 번째 Row방정식에서부터 해를 풀어나가는 것

2. 소거 행렬 + 행렬 곱셈

1. 소거 행렬(Elimination Matrices) 생성
2. 행렬 A에 곱하기

2.1 Elimination matrices (소거 행렬= E)

소거과정을 행렬의 곱으로써 만들어내는 것

소거 행렬을 $$ E_{21}$$이라고 표현한 이유는 A의 Row2/Col1(=값 3)을 0으로 만드는 것이 목적이므로

Step 1. Row1과 Row3은 그대로 유지 하기 위하여 I 행렬로 지정

Step 2. Row2는 A의 Row1에 3을 곱하고 Row2에서 이를 뺴준다. (Row3은 아무 역할도 안함)

Step 3. Row3은 A`의 Row2에 2를 곱하고 Row3에서 이를 뺴준다.

• 산출물은 U 행렬

최종 정리