Determinant Application
주로 cofactor와 관련있음
1. 역행렬(Inverse Matrix) 구하기
우리가 알고 있는 역행렬식을 행렬식을 이용하여 유도해 보자
$$ A^{-1}= \frac{C^T}{\det A} \rightarrow (\det A)I = AC^T$$
C = cofactor Matrix
2. 연립방정식의 해 구하기
크래머 공식(Cramer's Rule) 이용
- 목적 : 행렬식(determinant)를 활용하여 A의 역행렬 구하기
- 가우스 소거(Gauss Elimination)에 비해 대수적 공식(Algebraic Formula)으로 깔끔하게 정리된 것
- 하지만 속도는 가우스 소거가 더 빠름, 이런 공식이 있다는 것만 알아 두자
- 임의의 선형시스템 방정식(Linear System Equation) Ax=b의 해(solution) x를 행렬식(determinant)으로 유도된 공식을 통해 푸는 방법이다.
- 요구사항 : 정방행렬(square matrix),특이 행렬(singular matrix)이 아니어야 한다.(determinant를 이용하기때문)
| $$Ax=b$$ | $$x=A^{-1}b$$ | $$ x = \frac{1}{det A}C^Tb $$ |
|---|---|---|
| 원식 | 역행렬로 x도출 | determinant를 이용한 도출 C는 여인수행렬 |
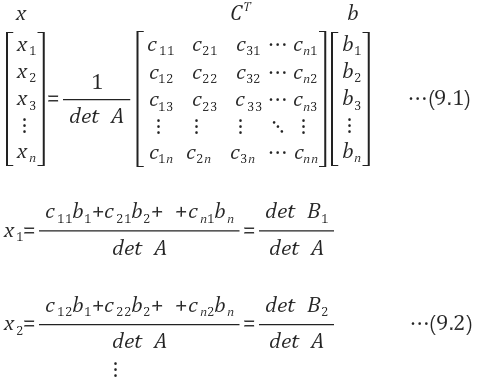 |
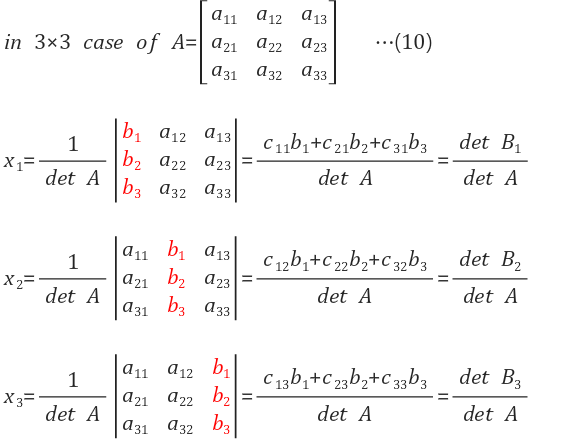 |
$$x_1 = \frac{det B_1}{det A}$$ |
| 풀어서 표현 | $$\frac{C^T행렬의 row 원소들과 b원소들을 내적(dot product)한 것}{A의 determinant}$$ | 결국, determinant로 문제 풀이 |
3. Volume of box
두 백터의 Determinant는 넓이를 의미함 세 백터의 Determinant는 부피를 의미함