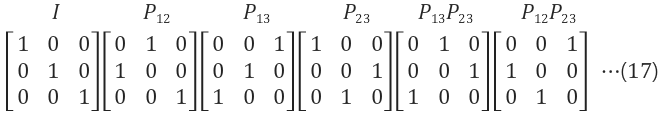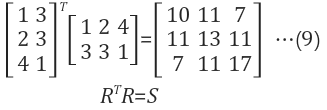치환 행렬
1. 정의
목적: 치환 행렬(Permutation matrix, P)은 행 교환(row exchange)을 수행하는 행렬
활용예 : 소거 과정에서 pivot이 0이 되는 경우에 행 교환이 필요하며 이때 사용되는 행렬이 바로 치환 행렬
2. 속성
치환 행렬은 편리한 속성이 두 가지 있다.
- 첫 번째는 모든 P행렬은 invertible하다. 즉 역행렬이 존재한다.
- 두 번째는 P행렬의 역행렬은 전치(Transpose)행렬과 같다. $$P^{-1}=P^T, P^TP=I$$
- has the same rows with Identity Matrix
- There is a single '1' in every rows and column
- 치환 행렬의 조합의 개수: n!(factorial). 즉 n=3, 3x2x1=6가지의 조합
- 다시 원래대로 되돌려 놓으려면 어떻게 해야 할까? 바로 역행렬을 곱함
3. 방법
3.1 2 x 2 행렬
| Row 치환 | $$P \times A$$ 왼쪽위치 |
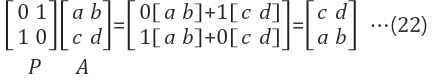 |
|---|---|---|
| Column치환 | $$A \times P$$ 오른쪽 위치 |
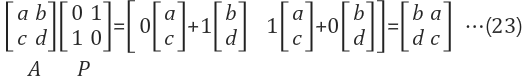 |
3.2 3 x 3 행렬에서 일부 행
- $$P_{21} $$ = 2번행렬와 1번 행렬을 서로 바꿈 $$ \begin{bmatrix}0 & 1 & 0 \1 & 0 & 0 \ 0 & 0 & 1 \end{bmatrix} $$
$$P^{-1} = P^{T} $$ :P의 역행렬은 Transform하면 된다.
Transpose (전치행렬)
1. 정의
row의 원소들이 column이 되고, column의 원소들이 row의 원소가 되는 것
대각선을 중심축으로 행렬을 180도 돌려서 뒤집는 것
$$ A^T = a{ij} -> a{ji} $$
2. 속성
$$ (A+B)^T = A^T + B^T$$
$$ (AB)^T = B^TA^T$$
$$(A^{-1})^T = (A^T)^{-1} $$
Symmetric Matrix (대칭행렬)
$$ A^T = A $$ : 전치해도 값이 같다.
if A is symmetrix and invertible, then $$ A^{-1}$$ is too
Correlation Matrix
- 자신과 관련된 정보 출력
$$ R = A^TA$$
$$ R^T = R $$
자신과 자신의 전치와의 곱은 내적과 같음
대칭행렬(Symmetric Matrix)
1. 정의
전치(Transpose)를 해서 행렬을 뒤집어도 원래 행렬과 같은 특성
$$A^T = A $$
2. 구하는 법
- $$S = R^T R $$ : 임의의 행력와 그의 전치 행렬을 곱함
[참고] 역행렬 & 전치 행렬
$$ AA^1 = I \rightarrow Traspose(전치)\rightarrow (AA^-1)^T = (I)^T \rightarrow (A^{-1})^T(A)^T = I \rightarrow (A^{-1})^T = (A^T)^{-1}
$$