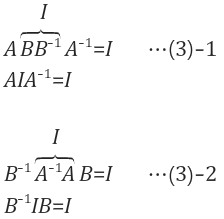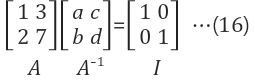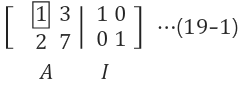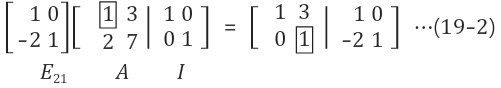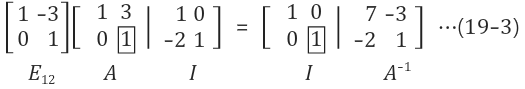Matrix multiplication (행렬 곱)
1 Row x column 방법
regular way – 성분 별 dot product
2 Column-wise방법
column way – 열들의 선형 결합
3 Row-wise 방법
row way – 행들의 선형 결합
4 column x row 방법
A 의 k 번째 열과 B 의 k 번째 행의 곱셈 결과 행렬들을 모두 더함
5 Block Multiplication 방법
Inverse(역행렬)
$$ AA^{-1} = A^{-1}A = I $$
보통 행렬은 곱셈의 순서에 따라 결과가 달라진다. 하지만, 역행렬이 존재 하는
정방행렬(Square Matrix)의 경우는 그렇지 않다.
한개 이상의 역행렬의 곱
역행렬 존재 요구 사항
만약, 가우스 소거법 결과과 N 개의 피폿을 생성할때 (=가우스 소거법이 가능하다)
The inverse is unique
if $$ A^{-1} $$ exists, Ax = b => $$AA^{-1}x = A^{-1}b $$
Assume that there is a non-zero vector X such that Ax = 0 (b=0) ==> then $$ A^{-1} $$ does not exist
- Diagonal Matrix의 역행렬은 $$ d_n -> 1/d_n $$
- 대각선은 0이 존재 하면 안된다. (곱해서 0이 되면 안됨)
- The inverse comes in the reverse order
- $$ (ABC)^{-1} = C^{-1}B^{-1}A^{-1} $$
역행렬이 존재 하지 않는 경우
- Ax = 0을 만족 하는 해가 있는 경우
- A는 정방행렬, x는 0이 아닌 백터
행렬식이 0이 되는 경우
Column picture에서 두 column이 같은 방향을 가르 키는 경우
1.1 역행렬 계산법 (2x2경우)
$$ A^{-1} = \frac{1}{ad-bc}\begin{bmatrix} d & -b \ -c & a \end{bmatrix}
$$
1.2 역행렬 계산 법 (3x3 이상의 경우) - Gauss-Jordan Method
A에 역행렬을 곱하면 I가 되어야 한다.
두개의 column wise시스템으로 분리 하면 아래와 같다.
두 식을 합쳐서 하나의 식으로 만든다. 이때, Augmented Matrix의 extra column를 두개로 한다.
Gauss소거법을 활용해 소거
반대로 아래에서 위쪽으로 소거를 한번 더 진행