직교 벡터
두 벡터가 직교(orthogonal) = 수직(perpendicular) = 두 벡터 사이의 각도가 90도
직교를 찾는 이유 = 벡터가 수직이면
- Linearly independent basis
- Easy calculation in linear combination
orthgonal vector = basis vector = span 가능
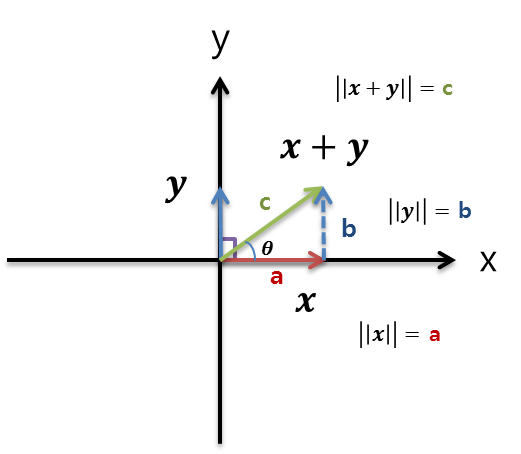
약간 다르게 표현하면 두 벡터가 직각삼각형(right triangle)을 이룬다
- lenght of vectors = $$\parallel X \parallel $$
-> $$ \parallel X \parallel ^2 = X^TX = \sum_{i=1}^n{x_i}^2 $$
피타고라스 정리
- $$ \parallel y-x \parallel ^2 = \parallel x \parallel ^2 +\parallel y \parallel ^2 $$
- $$ (y-x)^T(y-x) = x^Tx + y^Ty $$
| For vector inner product(내적,dot product=$$ x^Ty $$) |
|---|
| $$ x^Ty = 0 \rightarrow angle = 90도 $$) |
| $$ x^Ty < 0 \rightarrow angle > 90도 $$) |
| $$ x^Ty > 0 \rightarrow angle < 90도 $$) |
cosine때문에 두 벡터가 직교(orthogonal)할 경우 그 결과값이 0이됨
[참고]코사인 제2 법칙 |
|---|
| $$ \parallel b-a \parallel ^2 = \parallel a \parallel ^2 +\parallel b \parallel ^2 - 2\parallel a \parallel \parallel b \parallel \cos\theta $$ |
| $$(b-a)^T(b-a)=a^Ta + b^Tb - 2\parallel a \parallel \parallel b \parallel \cos\theta $$ |
| $$a^Tb =\parallel a \parallel \parallel b \parallel \cos\theta $$ |
2. 부분 공간의 직교(Orthogonality of subspaces)
Every vector in one subspace is orthogonal to every vectros in the other subspace
한공간에서 임의의 백터들과 다른 공간의 임의의 백터들이 항상 직교 하면, 두 공간은 직교 이다.
두 부분 공간이 직교하기 위해선 다음의 두 가지 조건
- S에 존재하는 모든 벡터가 T에 존재하는 모든 벡터와 직교해야 한다.
- 두 부분 공간이 만나는 점은 오직 원점(origin)에서만 만나야한다.
[참고] Orthogonal complement subspace
$$ v \in V, w \in W in R^n $$일때,
$$ v \perp w $$이면, Orthogonal subspace
또한, $$ Dim(V) + Dim(W) = n $$ 이면 Orthogonal complement subspace
조심 : Orthogonal subspace $$\neq$$ Orthogonal complement subspace