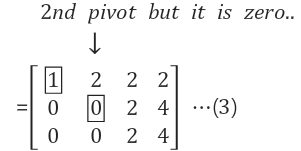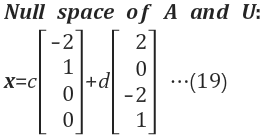Null Space 계산 알고리즘
- Ax = 0
- Ux = 0
- Rx = 0
| 기약행 사다리꼴을 통해 알수 있는 정보들 |
|---|
 |
| > A행렬을 줄이고 줄이고 줄여서 가장 간단한 형태인 R로 만들었다 |
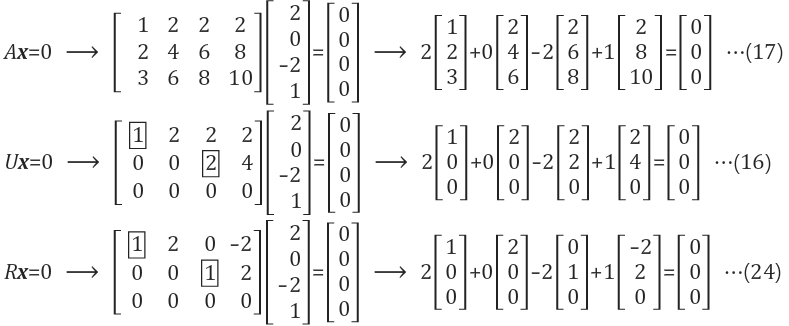 |
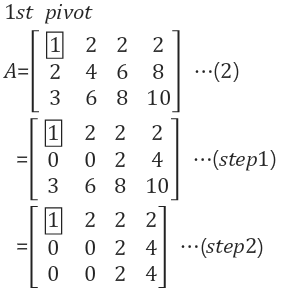
1. Ax=0풀기
소거를 통해 U구하기
Step. 1번쨰 피봇 계산
Step 1 : (2)에서 Low 1에 x2를 하여 Low 2를 뺀값 Step 2 : (2)에서 Low 1에 x3를 하여 Low 3를 뺀값
Step. 2번쨰 피봇 계산
두번째Row가 0임 -> 세번쨰 Row와 행교환필요 -> 세번째 Row도 0
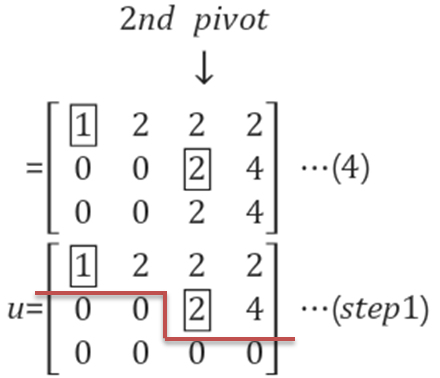
Step 1 : (4)에서 Low 2에 x(-1)을 하여 Low을 뺸값
진행은 하였지만, 역삼각형(Upper triangular matrix)이 아닌 계단형태, 이를 echelon form이라 함
| 중요 : 피봇의 갯수가 2개임을 파악 = 행렬 A의 Rank 는 2 | Rank of A = number of pivots |
|---|---|
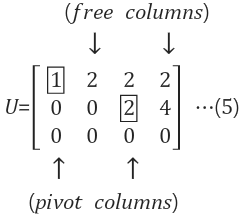
2. Ux = 0 풀기
2.1 Pivot column와 Free column 정의 하기
special solution : 임의의 free variable을 설정하여 구한 해(solution)
- 보통 첫 번재 free variable을 1로 놓고 나머지는 0, 그 다음은 두 번재 free variable만 1로 놓고 나머지는 0으로 설정하는 식으로 계산
2.2 Free column에 임이의 값 할당 후 후방대입법으로 풀기
free columns는 임이의 값을 자유롭게 설정 할수 있음
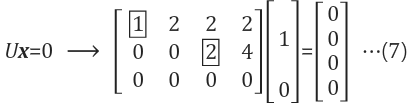
[special solution 예제] x2=1, x4=0을 할당
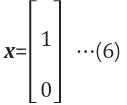 |
 |
|---|---|
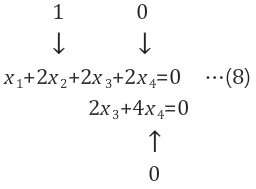 |
$$2x_3 = 0 \rightarrow x_3 = 0 $$ $$x_1=-2 $$ $$ X^T = {-2,1,0,0} $$ |
[special solution 예제] x2=0, x4=1을 할당
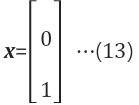 |
|
|---|---|
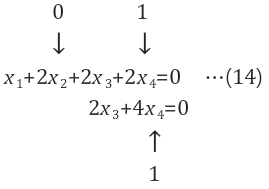 |
$$x_3=-2$$ $$x_1=2$$ $$ X^T = {2,0,-2,1} $$ |
2.3 해 확장
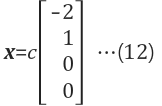 |
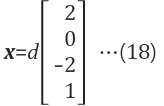 |
|---|---|
해에 상수 c를 곱하여 새로운 해 찾을수 있음
2.4 전체 Null Space 정의
두 개의 해의 선형 결합(Linear combination)으로 구할수 있음
Rx=0 풀기
기약행 사다리꼴 행렬(Reduced row echelon form, R)
Echelon form: 행렬 A를 소거하여 U를 만들때 U는 계단 형태일때
Reduced row echelon form: Echelon을 좀더 소거(간소화)한 형태
- pivot 원소들의 아래, 위로 모두 0이 되어야 한다
1. 만드는 법
Step 1. Pivot의 아래, 위를 모두 0으로 만듬
1을 곱해서 빼준다
Step 2. Pivot의 값을 모두 1로 만든다.
pivot이 있는 row전체를 pivot으로 나눠주면된다
| 기약행 사다리꼴 행렬이기 위한 조건 |
|---|
| . pivot 원소들은 반드시 1이 되어야 한다. . pivot 원소가 있는 column에서 pivot 변수의 모든 아래/위 원소들은 0이 되어야 한다. . 각 row는 처음 나오는 pivot 원소를 만나기 전까지 모든 원소가 0이어야 한다. . 모든 원소가 0인 row는 반드시 pivot 변수가 있는 row의 밑에 있어야 한다. |