투영

투영에 대한 응용으로써 최소자승법(Least square method)

최소자승법(Least Square Method)

1. Basics of Least Square

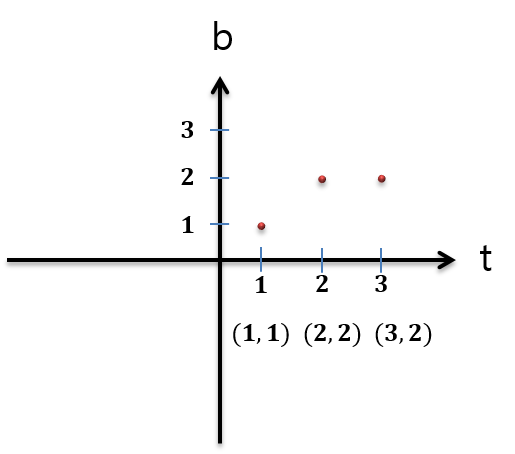
정의 : 수집한 데이터를 기반으로 이들 모두를 최대한 만족시키는 하나의 Line(예측용)에 대한 식을 찾는 방법

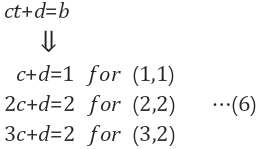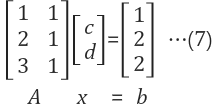하나의 라인은 y = ax + b로 표현 가능, - 표현법 변경 : b = ct + d	방정식으로 표현	Ax=b꼴로 변환 - overdetermined case -best solution = $$A^TAx = A^Tb$$
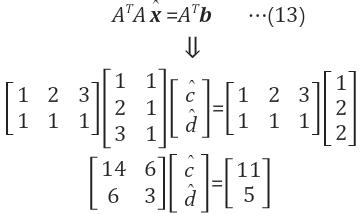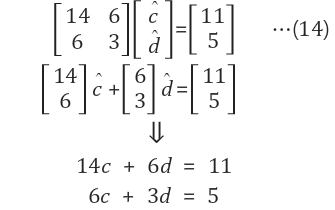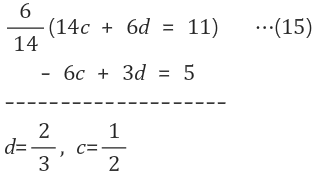x hat구하기 Ax=b의 양변에 A transpose를 곱해주자	일반적인 방정식	가우스 소거법을 활용하여 실제 해를 구하는 것
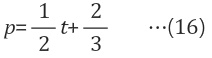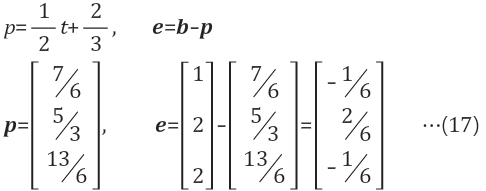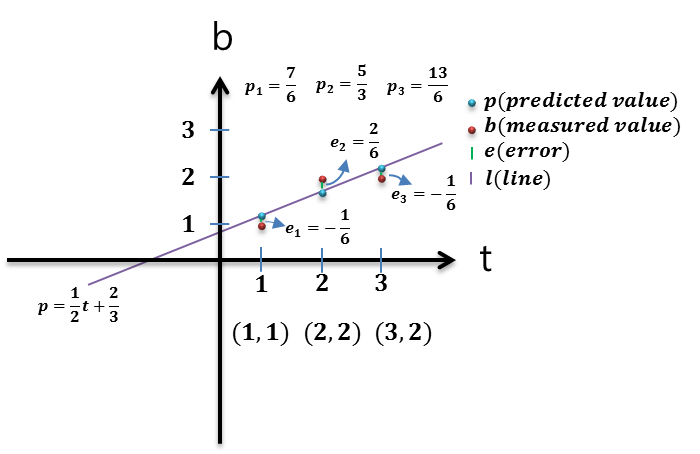$$\hat{x}=[\hat{c} \hat{d}]^T$$를 이용 최적의 라인(Line)에 대한 방정식 구하기	t=1, 2, 3을 대입하여 p1=7/6, p2=5/3, p3=13/6 구함 에러는 e=b-p이므로 b=1, 2, 2에서 p1, p2, p3를 각각 빼주면된다	최종 결론

• 직선을 완벽하게 관통하는 직선을 구하기는 어려움
• 각각의 데이터와의 에러를 최소화 하는 직선이 Best Solution임
• 에러 계산은 [좌변의 값]-[우변의 b값], 음수 상쇄 하기 위하여 $$ e^2$$ 수행