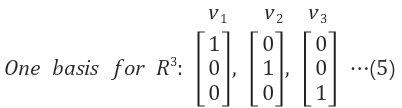선형 독립(Linear independence)
vector 들을 합해서 0을 만들 수 없다 = 독립적
vector 들을 합해서 0을 만들 수 있다 = 의존성
eg. 독립 : x(1, 1) + y(1, 0) = (0, 0)
- x = 0, y = 0일때만 0이된다.
종속 : x(1,1) + y(2,2) = (0, 0)
- x= 0, y = 0
- x = -2, y = 1 (0,0)이된다
참고
- 기저 : 선형독립 백터 집합, (1, 1), ( 1, 0 )
- 차원 : 기저의 원소의 개수
| 구분 | 독립(Independence) | 종속(Dependent) |
|---|---|---|
| 어떠한 선형 조합(Linear combination)으로도 0을 만들 수 없다 | 선형 독립 연산을 했을 때 결과 값이 0인 경우가 발생 | |
| 두 벡터 v1과 v2를 이용하여 어떠한 선형 조합을 한다해도 0을 만들 수는 없다 | 벡터 중 하나라도 0벡터일 경우 | |
| - 벡터들을 행렬 A의 column으로 넣고 행렬 A의 Null space를 체크. - 만약 이 행렬 A의 Null space(Ax=0)가 오직 zero vector만 존재할 경우, 이 벡터(행렬)들은 독립이다. - 이때의 행렬 A의 Rank는 column의 수 n과 같다. (Rank=n) - 따라서 free variable이 존재하지 않는다. |
- 벡터들을 행렬 A의 column으로 넣고 행렬 A의 Null space를 체크. - 만약 이 행렬 A의 Null space(Ax=0)가 zero vector이외의 다른 값이 존재할 경우, 이 벡터(행렬)들은 종속이다. - 이때의 행렬 A의 Rank는 column의 수 n보다 작다. (Rank |
Rank of A
정의 : Dim of Column space
수량
- Number of pivots in G.E
- Number of independent column vectors
- Number of independent row vectors
Span
벡터들을 이용하여 온갖 선형결합을 통해 만들어진 벡터 스페이스
Set of vectors constructs of vector space by linear combination
사전적 의미: "(많은, 넓은 것을)포괄하다, 걸치다, 가로지르다
- 선형대수 의미 : span a space, "어떤 공간을 포괄하다
벡터 v1, v2, ... vn이 어떤 공간(space)을 span한다의 의미
- 벡터 v1, v2, ... vn들의 가능한 모든 선형 조합으로 공간을 형성하는 것을 의미한다.
- 이때 형성되는 공간은 조합되는 벡터에 따라 Rn이 될 수도, 혹은 부분 공간(subspace)이 될 수도 있다.
- 벡터들의 모든 가능한 선형 결합(Linear combination)의 결과 벡터들을 하나의 공간에 몰아 넣은 의미한다.
- 사용하는 벡터에 따라서는 모든 공간을 채울 수도 있고, 혹은 2차원에선 Line, 3차원 공간에선 평면(Plane)과 같이 부분적인 공간만을 채울 수도 있는 것이다. 이러한 작업을 줄여서 "span"이라 한다.
Basis(기저) vector
1. 정의
- 벡터 공간에서 각각의 축방향을 가리키는 단위 벡터
- 각 축의 방향으로 크기가 1인 벡터
예
- 2차원의 기저 벡터 : $$<1,0>, <0,1> $$
3차원의 기저 벡터 : $$<1,0,0>, <0,1,0>,<0,0,1>$$
벡터들은 바로 어떤 공간을 "span"하면서 그들이 독립(Independent)인 벡터들이다.
Number of minimum linearly independent vectors to span the vectors span
- 기저(basis)는 유일하지 않다
2. 특징/속성
기저벡터들은 독립(Independent)이다.
기저벡터들은 공간(space)을 "span"한다.
기저를 쓰는 이유
- 물체가 아니라 기저를 회전 시키거나 이동시키면 결과적으로 물체가 이동,회전한 것과 같기때문!!
- 기저들을 이용해서 행렬을 만들어서 물체와 곱하면 연산을 아주 많이 줄일수 있기 때문이다!!
3. 예
독립이면서 3차원 공간 $$R^3$$를 "span"하는 벡터
- 독립 : v1, v2, v3에 어떤 상수들(c1, c2, c3)을 곱해서 더해도 영벡터를 만들 수 없다
- Span: 세 벡터의 선형조합을 통해 3차원 공간상의 어떠한 벡터도 만들어낼 수 있다
4. 기저 여부 확인법
- 먼저 벡터들을 어떤 행렬의 column vector로 만들어서 하나의 행렬을 만듬
- 가우스 소거(Gauss Elimination)를 통해 echelon form 행렬을 만듬
- 행렬이 free variable을 갖는지, 혹은 모든 각 column vector가 pivot을 가지고 있는지를 확인
- 즉 행렬의 Rank를 가지고 판별하는 것
n x n 행렬이 역행렬이 존재(invertible)해야 한다
차원
1. 정의
- 일반적 의미 : 선(Line)을 1차원, 면(Plane)을 2차원, 입방체(cubic)를 3차원
- 선형대수적 의미 : 주어진 공간(space)들에 대한 모든 기저(basis)들은 같은 수의 벡터를 가진다.
- 여기서 벡터의 수가 바로 그 공간의 차원(Dimension)을 의미한다.