Ax=b의 완전해(complete solution)
한양대 강의, 선형대수 7강 벡터의 선형독립과 기저벡터: 00:00 ~ 42:00
| Finding the solution Ax = b | |||
|---|---|---|---|
| 1 | [A\ | b] -가우스 소거법-> [R\ | d] . R=기약행렬 |
| 2 | Seperate : pivot variable & free variable | ||
| 3 | Find the Special solution for null space from R | ||
| 4 | Find the particular solution |
1. 해가 존재 하는지 알아 보기
가해 조건 확인
 |
 |
 |
|---|---|---|
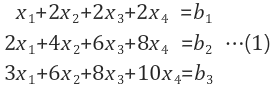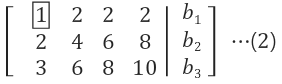
| 원식 | 매트릭스폼 | 소거 -[row2=row2-2row1] -[row3=row3-3row1] |
 |
 |
|
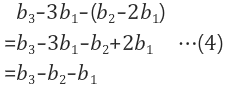| (row2, col3)의 아래원소를 2->0으로 row3=row3-row2 |
최종 U행렬 |
최종 u행렬의 row3을 보면 좌변 계수는 모두 0이다. 따라서 $$b_3 - b_2 - b_1 = 0$$이다.
- 계수가 전부 0이기 때문에 어떤 변수를 곱해도 결과는 당연히 0이 될 수 밖에 없다.
- 가해 조건(solvability condition)
- 선형방정식에 해가 존재하기 위한 조건
가해 조건을 확인해보는 것은 결국 이 선형방정식이 해가 존재하는지를 확인해보는 작업
2. 완전해 구하기
2.1 particular solution(특수해) x를 찾는다.
특수해 : 소거를 마친 행렬 U에서 free variable을 모두 0으로 만든 다음 pivot variable에 대해서 구한 해
 |
 |
 |
|---|---|---|
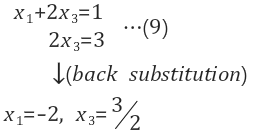| 식(8)에서 Free variables로 식(9)를 만듬 | free variable을 0으로 설정< 후방대입으로 $$ x_1=-2, x_3=\frac{3}{2}$$ 구함 |
Ax=b의 특수해 도출 |
2.2 Null Space해를 찾는다.
널스페이스 해 : Ax=0을 만족시키는 x
 |
|
|---|---|
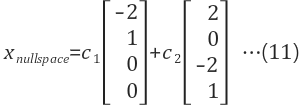| 7장 참고 | 최종 Null space 해 |
2.3 완전해 구하기 = 특수해 + 널 스페이스 해
Rank와 Solution
n = rank , m = # of rows, n = # of columns