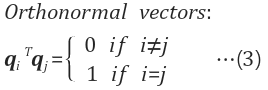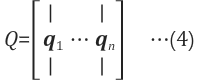직교행렬(Orthogonal Matrices)과 그람 슈미트 과정(Gram-Schmidt Process)

If given imdependent vectors a1, a2, a3.....an

  • find the Orthogonal basis vectors : 그람 슈미츠 과정 이용
  • Linear combination을 쉽게 처리 할수 있음

직교 행렬

  • 모든 column vector가 자기 자신을 제외한 나머지 모든 column vector들과 직교
  • 크기가 1인 단위 벡터들로 구성된 행렬

그람 슈미트 과정

  • 임의의 독립 행렬(independent matrix)로부터 각 column vector가 정규직교(Orthonormal)한 벡터들로 구성된 직교 행렬을 만드는 과정

1. 정규직교벡터(Orthonormal Vector)

1.1 단위 벡터(Unit Vector)

정의 : 길이가 1(단위길이)인 벡터 = 방향성분만을 나타내는 벡터 = 크기 성분에는 영향을 끼치지 않음

- 예 : 길이를 나타내는 2m에서 m는 길이를 나타내며 실제 길이에는 영향을 안 미침
일반벡터 -> 단위백터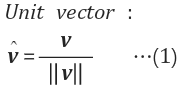
(예) $$v=[2 1 3]^T$$
-> 단위벡터

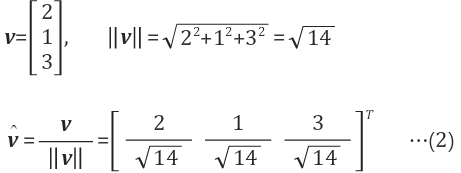단위 벡터 = 정규화 벡터(normalized vector)라고도 한다.

  • 즉 서로 다른 스케일을 가지고있는 벡터들을 동일한 스케일에서 바라보기위해 벡터의 크기로 나누어 정규화(normalization)한 벡터를 의미한다.

1.2 정규직교벡터(Orthonormal vector)

직교 벡터

  • 벡터 사이의 각도가 90도, 즉 직각(perpendicular)을 이루는 벡터
  • a와 b의 내적(dot product)은 0

정규직교벡터

  • 바로 직교 벡터(orthogonal vector)이면서 단위 벡터(unit vector)인 벡터
  • 두 벡터가 90도의 각도를 이루고, 각 벡터의 길이(크기)는 1인 방향성분만을 나타내는 벡터

  • qi는 자기 자신에게는 직교(orthogonal)하지 않는다.
  • qi를 자기 자신과 곱하면, 즉 자기 자신과 내적(dot product)하면 그 결과값은 1이 된다

이것이 의미하는 것은 q는 벡터의 크기가 1인 단위 벡터(unit vector)라는 의미다.

[예] 정규직교벡터(orthonormal vector)

  • sin과 cos으로 이루어진 벡터를 나타낸다.
  • 이들 벡터 a, b의 길이는 각각 1이며 둘 사이의 각도는 90도이다.

두 벡터가 직교(perpendicular)하며 각 벡터의 길이는 1로써 방향성분만을 나타내므로 이들은 정규직교벡터이다.

2. 직교행렬(Orthogonal Matrices)

2.1 Basic of Orthogonal Matrix

직교행렬(orthogonal matrix)

  • 행렬의 row와 column vector들이 자기 자신을 제외한 나머지 모든 row, column vector들과 직교(perpendicular)이면서 동시에 단위 벡터(unit vector)인 행렬
  • 즉 orthonormal vector들을 행렬 Q에 집어넣은 것과 같다

2.2 Square Orthogonal Matrix

직교 행렬(orthogonal matrix)이면서 정방행렬(square)인 경우의 가장 대표적인 예는 단위행렬(identity matrix)

2.3 Rectangular Orthogonal Matrix

2.4 Orthogonal Matrix 이용의 장점

투영행렬식에서 A대신 Q를 이용하면 수식이 간단해 진다.

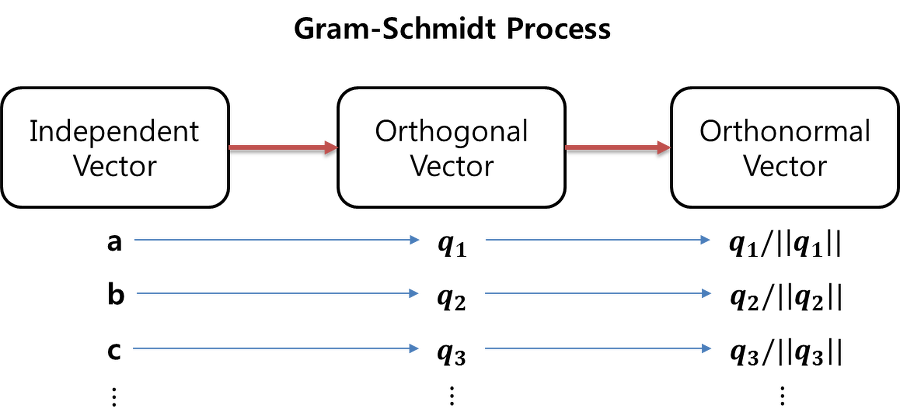
3. 그람-슈미트 과정(Gram-Schmidt Process)

한양대 Youtube 강의

그람-슈미트 과정(Gram-Schmidt Process): 행렬 A의 column vector를 orthonormal column들로 바꾸는 것

  • 즉 행렬 A를 정규직교벡터(orthonormal vector)들로 이루어진 직교 행렬(orthogonal matrix) Q로 만드는 것
그람-슈미트 과정은 이렇게 독립인 벡터들을 정규직교벡터로 만들어준다

  1. [그람(Gram)의 아이디어] a를 기준으로 a에 직교(orthogonal)한 벡터를 만들어낸다.

    • 이를 각각 q1, q2라고 하자. 즉 a->q1, b->q2로 만드는 것이다.

  2. [슈미트(schmidt)의 아이디어] 직교 벡터인 q1, q2를 정규직교벡터(orthonormal vector)로 만드는 것이다.

    • 이는 q1과 q2를 각각 자신의 크기로 나누어주면 된다.
1 첫번째 백터 a를 크기가 1이 되도록 Normalization $$a \rightarrow \frac{a}{ a } =q_1 $$
2 두번째 백터 b를 $$q_1$$에 투영
??

3.1 Making Orthogonal Vectors (by Gram)

3.2 Making Orthonormal Vectors (by Schmidt)

4. QR분해(QR decomposition)

그람-슈미트 방법(Gram-Schmidt Process)을 행렬로 정리하는 것

4.1 QR decomposition basic

A=LU 분해처럼 A=QR분해 하는것

  • Q행렬: 직교 행렬(orthogonal matrix)
  • R행렬: 상삼각행렬(Upper triangular matrix)의 형태를 띄고 있는 행렬

results matching ""

    No results matching ""