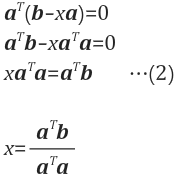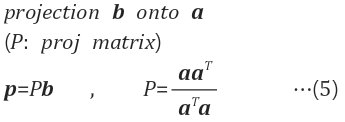투영행렬
투영
- 하나의 벡터를 다른 벡터로 옮겨서 표현
투영을 공부 하는 이유
- overdetermined case에서 근접한 해를 구하는 것이 목표
- 근접한 해를 구하기 위해 b를 A의 column space에서 가장 근접(=거리짧은)한 벡터로 치환(=투영)하여 문제 해결
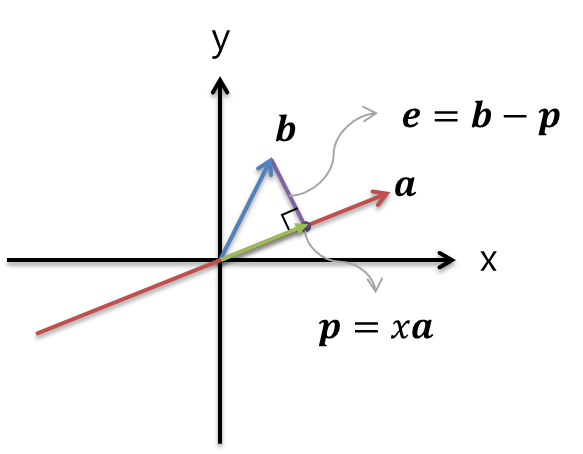
1. 2D-Vector Projection(2차원 벡터 투영)
두 벡터 a와 b를 나타내고 있다
A 투영(Projection, P)
- 초록색 백터, $$p=xa$$
- 스케일 상수 x를 찾는 것이 목표
- 벡터 b를 a에 투영시켰을 때 그 점이 벡터 a의 어느 지점에 위치할 것인가
- 즉, 벡터 a라는 1차원 공간의 어느 점이 벡터 b가 가리키는, 즉 벡터 b의 화살표 끝점과 가장 가까운지를 찾는 것이다.
- 벡터 b의 끝점에서 벡터 a의 수직(perpendicular) 방향으로 선을 그렸을 때 만나는 점
p는 다시 $$ ||b||\cos\theta$$로 표기 가능
p는 $$ A^TB 로도 표현?? $$
B 오차(Error, E)
- 보라색 백터, ($$e = b-p$$)
- 투영의 대상이 되는 벡터인 a와 직교(orthogonal)
C 투영시 스케일 상수 x 구하기
알고있는 점 1 : 벡터 a와 e가 수직(perpendicular)
- $$ a^T(b-xa) = 0 $$, $$ xa = p \rightarrow b-p = e(error)$$
- 백터 a와 백터 e의 내적 표현
- 수직이기 때문에 값은
0
1.1 Projection matrix(투영행렬) of n-dimensional vectors
A 사전 정보
$$ p = ax, x = \frac{a^Tb}{a^Ta} $$
$$ p = a\frac{a^Tb}{a^Ta} $$
위 식에서 알수 있는 점
- b가 두배로 늘어 나면, p도 두배로 늘어남
- a가 두배로 늘어 나면, p는 영향을 안 받음
B 표기법
b를 a로 투영시키는 투영행렬(projection matrix, P)
$$ (2.1 사전 정보 식에서) p= a\frac{a^Tb}{a^Ta} \rightarrow \frac{aa^T}{a^Ta}b
$$
분수식 앞의 a를 분자로 끌어올리고 b를 따로 떼어서 표기
소문자 p는 투영된 벡터이고 대문자 P는 투영 행렬
1.2 투영행렬 속성
- 투영 행렬의 rank는 1
- 대칭 행렬(symmetric matrix)
- P의 제곱은 P와 같다