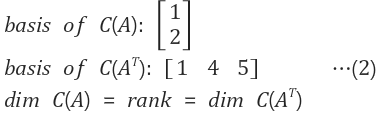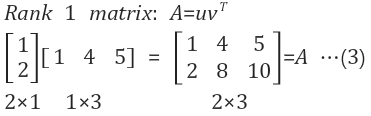Rank

1. 정의 / 속성

• 어떤 행렬을 소거했을 때 만들어지는 pivot의 개수
• 행렬이 표현할 수 있는 차원(dimension)을 의미
• rank는 m by n 크기의 행렬에서 반드시 m보다 작거나 같고, n보다 작거나 같다.

2. Rank 1 행렬(rank 1 matrices)

$$ A = \begin{bmatrix} 1 & 4 & 5 \ 2 & 8 & 10 \end {bmatrix}$$

- 종속 여부

row1과 row2는 서로 종속(dependent)

• 이유 : row1이 [1 4 5]이고, row2가 row1의 두 배인 [2 8 10]이다
• 같은 선상에 위치한다

col1, col2, col3는 서로 종속(dependent)

• 이유 : col2와 col3는 col1에 상수 4, 5를 곱한 것과 같기 때문
• col1과 일직선상에 위치

결론 : Rank 1인 행렬이 표현할 수 있는 공간은 1차원이며 직선

- 기저는?

row space의 기저(basis)는 row1이다. column space의 기저 역시 col1이다.

• 따라서 A의 row space와 column space의 차원(dimension)은 1로 같다.

- column x row = Rank 1 행렬 A

building block = Rank 1행렬은 벽돌 건물로 치자면 집짓기블록(building block)과 같은 것
즉 모든 행렬에 있어서 가장 작은 기본 단위의 요소와 같다
eg. - 5 x 14크기의 행렬 - rank가 4라면 4개의 rank 1 행렬의 조합으로 이를 표현할 수 있다

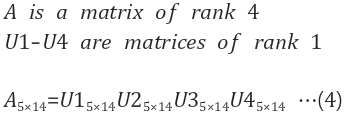3. Rank 1 행렬의 Subspace

3.1 차원(dimension) in R2

• row space: r=1
• null space: n-r = 2-1 = 1
• column space: r=1
• left null space: m-r = 1-1 = 0

3.2 기저(basis) in R2

• row space: [1 1]
• null space: [1 -1], [-1 1], ...
• column space: R1
• left null space: [0], empty