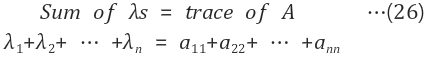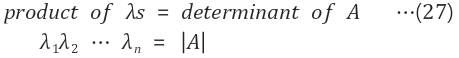고유값(eigenvalues)과 고유 벡터(eigenvectors)

벡터 공간을 간단히 표현해주는 방법 제공
- 임의의 정방행렬(square matrix) A에 대한 특별한
숫자가 고유값(eigenvalue,$$\lambda{} $$) - 임의의 정방행렬(square matrix) A에 대한 특별한
벡터가 고유벡터(eigenvector)- N x N행렬의 경우 N개의 고유 백터를 가짐
cf. Determinat :
고유값과 고유벡터는 그 행렬의 굉장히 중요한 정보를 담고 있다.
- 임의의 벡터를 어느 방향으로 얼마만큼 변화시키는지,
- 변환과정에서 변화 없이 유지되는 부분은 어느 부분인지 등이다.
활용예
- 영상이나 물체가 어떤 식으로 변환되고 중심축은 어디인지 등에 관한 중요한 정보들을 파악할 수 있다.
- PCA(Principal Component Analysis), 영상에서 EigenFace, 진동 분석(Vibration Analysis)
1. 고유값(Eigenvalue)과 고유 벡터(Eigenvector)
$$ Ax = \lambda{x} \Rightarrow \begin{bmatrix}2 & 3 \2 & 1 \end{bmatrix} \times \begin{bmatrix}3 \2 \end{bmatrix} = \begin{bmatrix}12 \8 \end{bmatrix} = 4 \times \begin{bmatrix}3 \2 \end{bmatrix}
$$
- A는 정방 행렬, (고유 벡터 존재시 변환 행렬 역할)
- x는 벡터, 행렬 A의 $$\lambda$$에 대한 고유 벡터
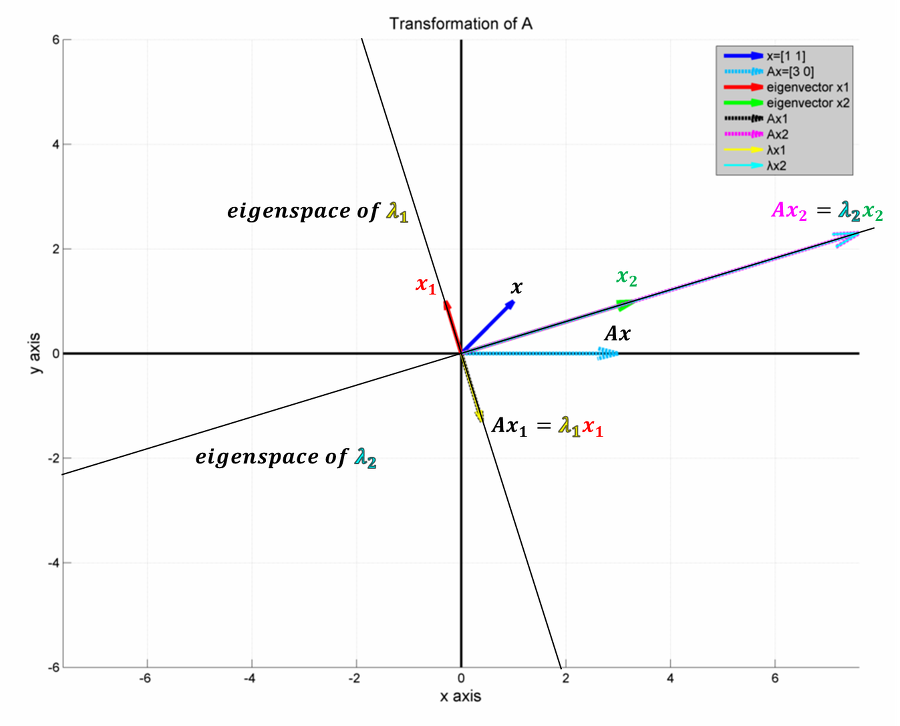
- 일반 벡터 : x가 A를 만나게 되면(Ax) 원래의 x와는 다른 방향으로 변환된다.
- 고유 벡터 : x가 A를 만나도 이전과 동일or평행(parallel).즉, $$A_X$$ parallel to $$_X$$
- $$\lambda$$는 행렬 A의 고유값(eigenvalue), 크기를 나타내는 특정 상수 (eg. 4)
고유 벡터 : $$x_1$$과 $$x_2$$
- 고유 백터에 A를 곱하여도($$Ax_1$$, $$Ax_2$$) 결과의 방향이 같다.
- 단, 크기와 반대방향은 변하였다.
 |
 |
|---|---|
1.1 고유값의 특징 (rules of eigenvalue)
A. 고유값의 합
고유값들의 합은 식 (22)의 행렬 A의 대각 원소(diagonal elements)들의 합, 즉 trace와 같다
B. 고유값의 곱
임의의 nxn 행렬 A의 행렬식(determinant)이 바로 고유값들의 곱(product of eigenvalues)과 같다는 것
1.2 고유 벡터 특징
A. 고유 벡터는 정방 행렬에만 존재
정방 행렬에만 고유 벡터가 존재 한다.
- 고유 벡터가 없는 정방 행렬도 있다.
N x N 정방 행렬일 경우 N개의 고유 벡터가 존재
B. 스케일 처리를 해도 결과가 같다.
고유벡터는 변환행렬로 곱하기 전에 고유벡터를 어떤 값(x2)으로 스케일 처리(곱/s나누기)를 해도 같은 값(4)을 곱한 결과가 된다.
$$\begin{bmatrix}2 & 3 \2 & 1 \end{bmatrix} \times \begin{bmatrix}3 \2 \end{bmatrix} = \begin{bmatrix}12 \8 \end{bmatrix} = 4 \times \begin{bmatrix}3 \2 \end{bmatrix}$$
$$ 2 \times \begin{bmatrix}3 \2 \end{bmatrix} = \begin{bmatrix}6 \4 \end{bmatrix} \Rightarrow \begin{bmatrix}2 & 3 \2 & 1 \end{bmatrix} \times \begin{bmatrix}6 \4 \end{bmatrix} = \begin{bmatrix}24 \16 \end{bmatrix} = 4 \times \begin{bmatrix}6 \4 \end{bmatrix}$$
C. 각 고유벡터들은 서로 수직이다.
D. 고유벡터의 크기는 1 (??)
2. 고유 공간 (eigenspace)
고유 값과 고유 백터는 유일한가?
- 교유값은 유일
- 교유백터는 무한히 많음
무수히 많은 고유백터들이 형성하는 공간이 고유 공간임
- nxn 행렬 A는 n개의 부분 공간인 고유공간(eigenspace)
[참고] Null Space에서의 고유값과 고유벡터
$$ Ax = \lambda{x} $$ : 고유값 $$\lambda{x}$$는 양수, 음수, 복소수, 0이 될수 있다.
만일 0이라면, $$ Ax = 0x \rightarrow Ax = 0$$
- 즉,이때의 고유벡터(eigenvector)는 영공간(null space)에 존재하는 것이다.
- 이말은, A가 특이 행렬(singular matrix)이란 뜻이다.
- 왜냐 하면, 정방행렬에서 null space가 존재하기 위해선 free variable이 존재하는 행렬, 즉 full rank가 아니어야하기 때문이다.
| 정리 : A가 특이 행렬인 경우 null space가 존재하고, 이때의 고유값인 람다는 0이 된다 |
|---|
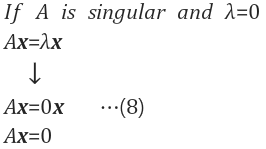 |
3. 계산 방법
3.1 블로그
  |
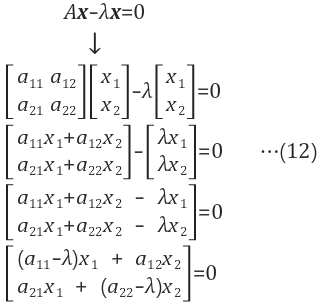 |
|---|---|
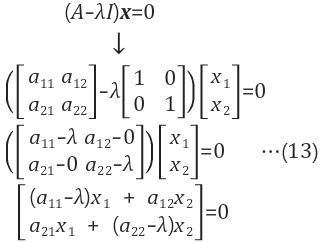 |
3.2 Youtube
| Null Space구하는 문제 |
|---|
| $$(A-\lambda{I})x = 0 $$ |
| X:eigenvector $$\rightarrow N(A-\lambda{I})$$ |
A. 고유값 구하기
Step 1. 원식
$$A = \begin{bmatrix} 4 & -5 \ 2 & -3 \end {bmatrix}$$
Step 2. 대각선에 교유벡터 뺀 Determinat=0
$$ \det (A-\lambda{I}) $$ = $$ \begin{bmatrix} 4-\lambda & -5 \ 2 & -3-\lambda \end {bmatrix} = 0 $$
$$ \lambda $$
$$(4-\lambda)(-3-\lambda)+10=0$$
Step 3. 연립 방정식으로 풀기
$$\lambda$$ = 2, -1
B. 고유 벡터 구하기
가. $$\lambda = 2$$ 일때 $$x_1, x_2$$ 구하기
$$\begin{bmatrix} 4-2 & -5 \ 2 & -3-2 \end {bmatrix} \rightarrow \begin{bmatrix} 2 & -5 \ 2 & -5 \end {bmatrix} \begin{bmatrix} x_1 \ x_2 \end {bmatrix} = \begin{bmatrix} 0 \ 0 \end {bmatrix}$$
$$2x_1 -5x_2 = 0$$
나. $$\lambda = -1$$ 일때 $$x_1, x_2$$ 구하기
4. 여러 행렬의 고유값과 고유벡터
4.1 치환행렬(permutation matrix)
4.2 대칭행렬(symmetric matrix)
[참고] Relationship between diagonal components of a matrix and eigenvalues
대칭행렬은 기존의 치환행렬에 3I(3 x Identity matrix)를 더한 것과 같다. 즉 치환행렬의 대각 원소들에 3씩 각각 더한 것이 식 (33.2)의 대칭행렬
고유벡터에는 영향을 주지 않는다. 그러나 고유값에는 바로 이 더한 만큼의 차이가 난다.
어떤 행렬의 대각원소에 어떤 값을 더하거나 빼주게 되면, 그 값만큼 고유값에 영향을 미치게되고, 고유벡터에는 영향을 주지 않는다
5. Caution in eigenvalues/eigenvectors
결론적으로 고유값/고유벡터에 있어서 행렬끼리의 덧셈, 곱셈은 선형성(Linearity)를 만족하지 않는다