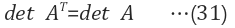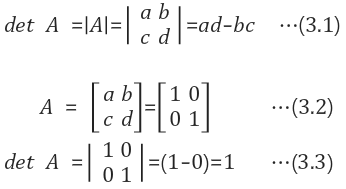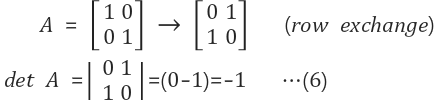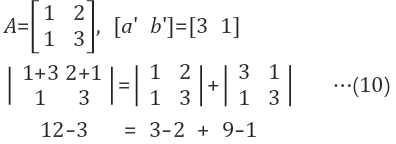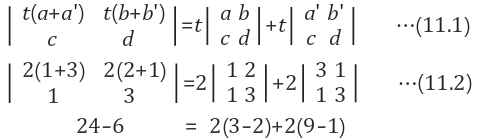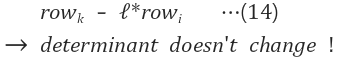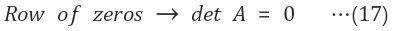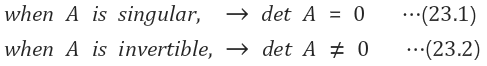행렬식의 특성(Properties of Determinants)
주요 특징
- 행렬에 역행렬이 존재 하면 행렬식은 0이 아니다. (역행렬이 존재 하는지 파악 가능)
- det A equals volume of a box in R^n
- determinat = $$\pm $$ (product of the pivot) = pivot들의 곱으로 이루어지는 수치
- square matrix에서만 정의되는 숫자
주요 활용
- $$ A^{-1}계산 $$
- $$ Ax =b $$
- Cramer's Rule : 해 x를 행렬식을 이용하여 계산 가능
- $$Ax=b \rightarrow x_i = \frac{\det{A_i}}{\det{A}}$$
- Volume of a Box
- A Formula for the pivots
| 본 정리에서는 행렬식(\ | A\ | )과 행렬([A])의 혼돈을 막기 위해 행렬식을 determinant 원어를 써서 표현 |
|---|---|---|
| $$ determinant notation: \rightarrow det A, \mid{A}\mid $$ |

1. 단위 행렬 특성
| 3 Basic Properties |
|---|
| 1. det I = 1 2. det A changes the sign when to rows are intercjamged 3. det A depends linearly on the first row |
단위 행렬(Identity matrix)의 determinant는 1 : $$det I = 1$$
2. Row 교환 특성
row를 교환하면 determinant의 부호가 바뀐다
row exchange의 횟수가 홀수번(odd)이면 -1, 짝수번(even)이면 부호는 그대로
3. (가칭)특정 Row 특성
3.1 (가칭)특정 Row에 상수 곱 특성
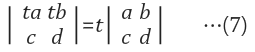
3.2 (가칭)특정 Row에 벡터 합 특성
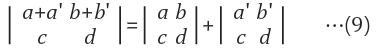
3.3 (가칭)특정 Row연산 결론
- 어느 하나의 row에 scale상수를 곱하거나 임의의 row벡터를 더했을 경우, 나머지 n-1의 row들은 그대로 둬야 한다는 것
- determinant를 구하는데 있어 선형 결합(Linear combination)의 규칙이 작용하는 것이다. determinant는 선형 함수(Linear Function)이다
위 1,2,3이 주요 특성이고 이후 특성은 1,2,3을 이용한 확장 특성
4. 동일 Row 존재시 특성
행렬 A에 똑같은 row가 2개 존재한다면 그 행렬의 determinant는 0이 된다
eg. 10 x 10의 정방행렬에서 row 2와 row 7이 같다 = determinant가 0
5. 소거 과정시 값 불편의 특성
- 행렬 A를 소거하여 상삼각행렬(Upper triangular matrix) U를 만들었을 때, U의 determinant는 A의 determinant와 동일
- 결국 행렬 A를 소거를 해도, 소거 과정에서 나오는 어떠한 행렬도 determinant는 변하지 않는다
6. 모두 0인 Row 존재시 특성
- 원소들이 모두 0인 row가 하나 라도 존재한다면 determinant가 0
7. 상삼각행렬의 특성
상삼각행렬의 determinant는 대각 원소 d1, d2, ... dn들의 곱으로 구할 수 있다
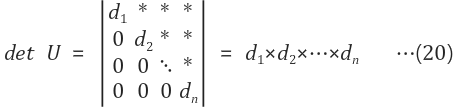
8. 특이행렬/역행렬 특성
- 행렬 A가 특이 행렬(singular matrix)일 때 determinant가 0이 되고
- 행렬 A가 특이 행렬이 아닐(=역행렬 가짐)때는 determinant가 0이 아니다.
9. 행렬의 곱과 determinant곱 간의 동등 특성
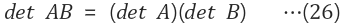
10. transpose의 특성