행렬식(Determinant)의 계산 방법

1. Product of all pivots from G.E

가우스 소거법으로 U로 바꾸어 대각선의 Pivot을 곱하여 계산
(행교환 없을 경우) A = LDU에서 $$\rightarrow$$ det a = det L x det D x det U $$\rightarrow$$ 1 x $$ \prod_{i=1}^n P_i $$ x 1
(행교환 있을 경우)PA = LDU $$\rightarrow$$ det p = $$\pm 1 $$

$$\begin{bmatrix} a & b \ c & d \end {bmatrix}$$ = ad -bc

Big Formula

Big formula를 분할하는 방법

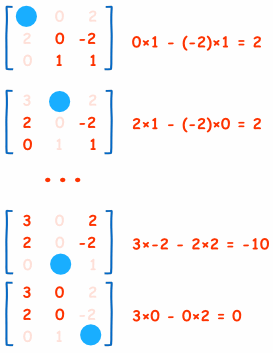
정의($$C{11}$$) : $$a{11}$$ 요소가 포함된 행열을 제외한 값을 이용해 submatrix를 만들고, 이 submatrix의 def 를 여인수라 함

$$ C{ij} = (-1)^{i+j} \det M{ij} $$

M= Minor maxtix = submatrix

여인수를 이용하여 def A구하기

$$ \det A = \sum{j=1}^{n} a{ij}C{ij} = \sum{j=1}^{n} a{ij}(-1)^{i+j} \det(M{ij}) $$