해가 존재하지 않는 선형연립방정식 Ax=b

해가 없기 때문에 아주 정확한 해(exact solution)는 구할 수 없지만 가장 근사한 해(Best Solution)를 구하는 것

1. Overdetermined 행렬

• M>N형태이므로 직사각형 모양

2 $$ AA^T $$의 특성

• Square Matrix: 정사각형 모양 $$\rightarrow$$ (N x M)(M x N) = N x N 형태
• Symmetric Matrix : 전치를 해도 자기 자신과 같음
• Invertible (if Full rank) : 정방행렬이면서 full rank이면 역행렬(Inverse matrix) 존재

3 Best Solution 도출 (Best solution for overdetermined equation)

$$ Ax =b (m>n)$$	$$ A^TA\hat{x}=A^Tb $$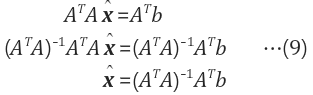
원식	양변에 $$A^T$$곱하기 hat($$\hat{} $$) = 최적해의미	Full rank이면 역행렬 존재 역행렬을 구하여 양변에 곱하기

3.1 Best Solution 도출 예시

4. when the solution exists in overdetermined equation

아무리 overdetermined 방정식이라도 해가 존재할 경우가 있다.

바로 우변의 벡터 b가 행렬 A의 column space에 존재할 때이다.

즉 A의 column 벡터들의 선형 조합(Linear combination)으로 b를 만들 수 있을 때를 말한다

5. Not invertible case

최적해(best solution)조차 구할 수 없는 경우

행렬 A의 column이 dependent할 때

Overdetermined system(m>n)에서 그나마 최적해라도 구하려면 행렬의 rank가 최소한 n과 같아야한다. 그러나 rank가 n보다 작을 경우엔 이 조차 불가능하다