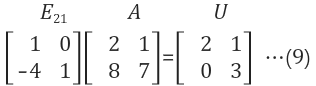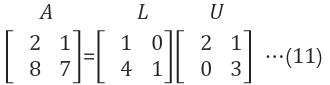LU 분할
1 용어 정리
분할(Decomposition/Factorization)이란
어떤 행렬(Matrix)을 여러 행렬들의 곱으로 표현하는 것 = cf.인수분해
- 인수 분해 : 방정식을 좀 더 알아보기 쉽게, 특수한 상황에서 문제를 풀기 쉽게
목적
- 첫 번째는 계산의 편리함(computational convenience)
- 두 번째는 분석적 용이성(analytic simplicity)을 위함
방법
- SVD(Singular Value Decomposition)
- QR Decomposition
- LU Decomposition
LU Decomposition
행렬A를 하삼각 행렬(L)과 상삼각행렬(U)의 곱으로 분해 하는것 = $$A = L U $$
가우스 소거(Gauss Elimination)에 의한 Elimination 행렬 형태로 볼 수 있으며, 때때로 치환행렬(permutation matrix)을 포함하기도 한다.
컴퓨터는 square 형태의 선형 방정식을 계산할 때 이 LU Decomposition을 사용하며, 역행렬(Inverse Matrix)을 계산하거나 행렬식(determinant)을 계산할 때 필요한 주요 과정이다.
2. LU 분할
A에 소거법을 적용하여 U행렬 생성
A= LU 를 이용하여 E의 역은 L임을 확인
$$
EA = U \rightarrow A = E^{-1}U \rightarrow E^{-1} = L
$$
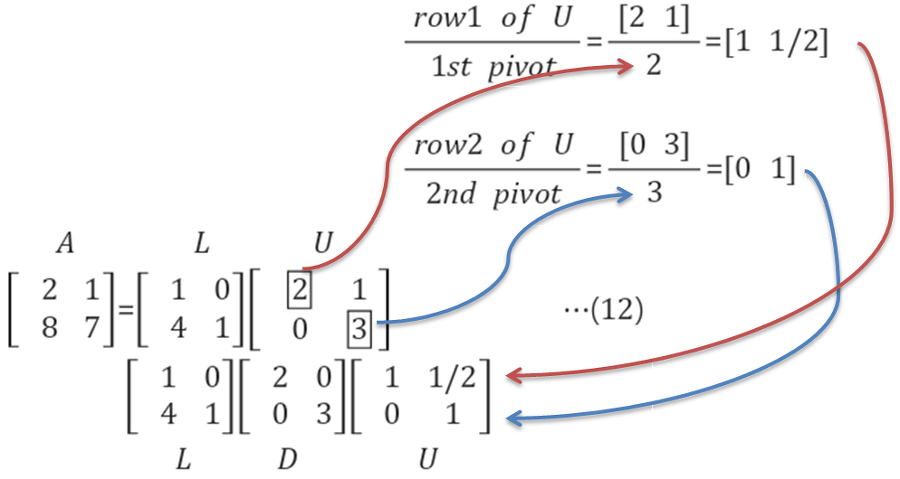
3. LDU 분할
Pivot들만 따로 떼어서 분해해야 하는 경우
A = L+ D + U = 하삼각행렬(Lower Triangular Matrix) + Pivot들만 있는 대각행렬(Diagonal Matrix)+ 상삼각행렬(Upper Triangular Matrix)
D 생성 : pivot만 떼어내어서 생성
U 변경
| 행교환 필요 유무 | 공식 | 방법 |
|---|---|---|
| 없음 | A=LU | 위의 기본 방식(2,3) |
| 필요 | PA=LU | 치환행렬(p)을 곱해 줌(4) |
1.5 Triangular Factors
$$ A x = b $$
$$ A = LU $$
Lower Triangular matrix * Upper Triangular matrix
? 가우시안 소거법을 행렬로 표현 -> Elementary Matrix $$ E{31}E{21} A $$ => U (upper triangular matrix)
Elementary Matrix in GE
$$ E{21} = \begin{bmatrix}1 & 0 & 0 \-l{21} & ? & ? \0 & 0 & 1 \end{bmatrix}
$$
해석 : 2번식 - (1번식 * $$L_{21}$$)
[참고]
$$ E{21}^{-1} = \begin{bmatrix}1 & 0 & 0 \l{21} & 1 & 0 \0 & 0 & 1 \end{bmatrix}
$$
$$ E{21}E{21}^{-1} = I $$
LU는
$$ E{32}E{31}E_{21}A = U
$$
$$ A = E{32}^{-1}E{31}^{-1}E_{21}^{-1} U
$$
$$ \begin{bmatrix}1 & 0 & 0 \l_{21} & 1 & 0 \0 & 0 & 1 \end{bmatrix}
\begin{bmatrix}1 & 0 & 0 \0 & 1 & 0 \l_{31} & 0 & 1 \end{bmatrix}
\begin{bmatrix}1 & 0 & 0 \0 & 1 & 0 \0 & l_{32} & 1 \end{bmatrix} U
$$
$$ \begin{bmatrix}1 & 0 & 0 \l{21} & 1 & 0 \l{31} & l_{32} & 1 \end{bmatrix} = Lower Triangular matrix = L
$$
LU 예시
$$ A = \begin{bmatrix} 1 & 2 \ 3 & 8 \end{bmatrix}
$$
2번식 - (3번식) x 1
$$ U = \begin{bmatrix} 1 & 2 \ 0 & 2 \end{bmatrix}
$$
$$ L = \begin{bmatrix} 1 & 0 \ 3 & 1 \end{bmatrix}
$$
? Diagonal matrix(D) = A = LU = LDU